题目内容
已知向量m= ,n=
,n= .
.
(1)若m·n=1,求cos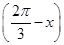 的值;
的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
 ,n=
,n= .
.(1)若m·n=1,求cos
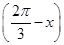 的值;
的值;(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
(1) cos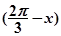 =-cos
=-cos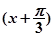 =-
=-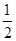 ;(2)函数f(A)的取值范围是
;(2)函数f(A)的取值范围是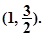
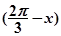 =-cos
=-cos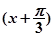 =-
=-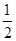 ;(2)函数f(A)的取值范围是
;(2)函数f(A)的取值范围是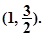
本试题主要是考查了向量的数量积公式和解三角形的综合运用。
(1)因为m·n=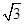 sin
sin 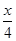 ·cos
·cos 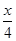 +cos2
+cos2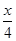 =
=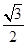 sin
sin 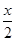 +
+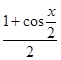
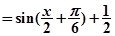 得到结论。
得到结论。
(2)∵(2a-c)cos B=bcos C,由正弦定理得(2sin A-sin C)cos B=sin Bcos C,
∴2sin Acos B-sin Ccos B=sin Bcos C.∴2sin Acos B=sin(B+C).
得到B的值,然后结合定义域求解值域。
解:(1) m·n=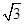 sin
sin 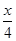 ·cos
·cos 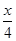 +cos2
+cos2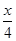 =
=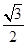 sin
sin 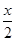 +
+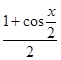
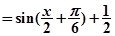 ,
,
∵m·n=1,
∴sin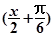 =
=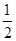 . cos
. cos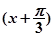 =1-2sin2
=1-2sin2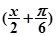 =
=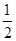 ,
,
cos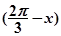 =-cos
=-cos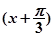 =-
=-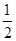
(2) ∵(2a-c)cos B=bcos C,
由正弦定理得(2sin A-sin C)cos B=sin Bcos C,
∴2sin Acos B-sin Ccos B=sin Bcos C.
∴2sin Acos B=sin(B+C).
∵A+B+C=π,∴sin(B+C)=sin A≠0.
∴cos B=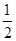 ,∵0<B<π,∴B=
,∵0<B<π,∴B=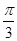 ,
,
∴0<A<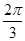 , ∴
, ∴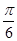 <
<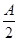 +
+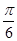 <
< ,sin
,sin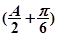 ∈
∈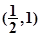 .
.
又∵f(x)=sin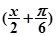 +
+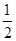 .
.
∴f(A)=sin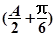 +
+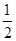 ,
,
故函数f(A)的取值范围是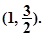
(1)因为m·n=
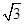 sin
sin 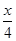 ·cos
·cos 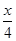 +cos2
+cos2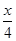 =
=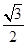 sin
sin 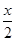 +
+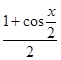
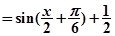 得到结论。
得到结论。(2)∵(2a-c)cos B=bcos C,由正弦定理得(2sin A-sin C)cos B=sin Bcos C,
∴2sin Acos B-sin Ccos B=sin Bcos C.∴2sin Acos B=sin(B+C).
得到B的值,然后结合定义域求解值域。
解:(1) m·n=
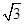 sin
sin 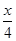 ·cos
·cos 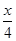 +cos2
+cos2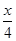 =
=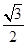 sin
sin 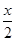 +
+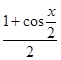
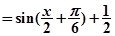 ,
,∵m·n=1,
∴sin
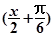 =
=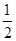 . cos
. cos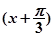 =1-2sin2
=1-2sin2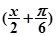 =
=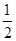 ,
,cos
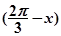 =-cos
=-cos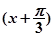 =-
=-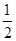
(2) ∵(2a-c)cos B=bcos C,
由正弦定理得(2sin A-sin C)cos B=sin Bcos C,
∴2sin Acos B-sin Ccos B=sin Bcos C.
∴2sin Acos B=sin(B+C).
∵A+B+C=π,∴sin(B+C)=sin A≠0.
∴cos B=
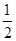 ,∵0<B<π,∴B=
,∵0<B<π,∴B=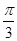 ,
,∴0<A<
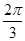 , ∴
, ∴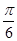 <
<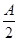 +
+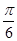 <
< ,sin
,sin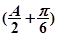 ∈
∈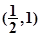 .
.又∵f(x)=sin
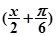 +
+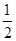 .
.∴f(A)=sin
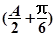 +
+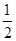 ,
,故函数f(A)的取值范围是
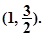

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
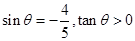 ,则
,则 .
.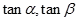 是方程
是方程 的两个根,则
的两个根,则 的值为
的值为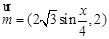 ,
,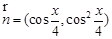 .函数
.函数 .
.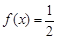 ,求
,求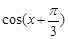 的值;
的值;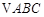 中,角
中,角 的对边分别是
的对边分别是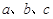 ,且满足
,且满足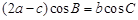 ,
,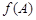 的取值范围.
的取值范围.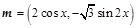 ,
,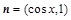 ,设函数
,设函数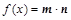 ,
,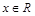 .
.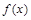 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;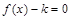 在区间
在区间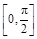 上有实数根,求
上有实数根,求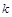 的取值范围.
的取值范围. ,
, ,则
,则 的值为________.
的值为________. 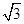 sinA-cos
sinA-cos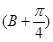 的最大值,并求取得最大值时角A,B的大小.
的最大值,并求取得最大值时角A,B的大小.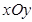 中,以
中,以 轴为始边作两个锐角
轴为始边作两个锐角 、
、 ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于 、
、 两点.已知
两点.已知 ,
,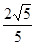 .
.
 的值;
的值; 的值.
的值. ,且
,且 ,则
,则 的值为
的值为