题目内容
已知函数 为奇函数,且
为奇函数,且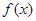 在
在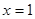 处取得极大值2.(1)求函数
处取得极大值2.(1)求函数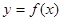 的解析式;
的解析式;
( 2)记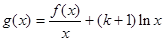 ,求函数
,求函数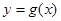 的单调区间;
的单调区间;
(3)在(2)的条件下,当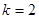 时,若函数
时,若函数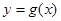 的图像的直线
的图像的直线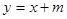 的下方,求
的下方,求 的取值范围。
的取值范围。
(1)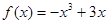 ;(2)见解析;(3)(1,+∞).答
;(2)见解析;(3)(1,+∞).答
 也正确.
也正确.
【解析】(1)f(x)是奇函数,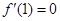 .可得a,b,c的值。进而确定y=f(x)的解析式。
.可得a,b,c的值。进而确定y=f(x)的解析式。
(2)先求出y=g(x)的表达式,然后求导研究单调区间即可。若遇参数可能要涉及讨论。
(3)解本题的关键是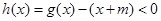 恒成立,然后利用导数研究h(x)的最大值即可。
恒成立,然后利用导数研究h(x)的最大值即可。
解:(1)由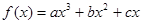 (
(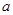 ≠0)为奇函数,
≠0)为奇函数,
∴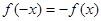 ,代入得,
,代入得,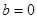 1分
1分
∴ ,且
,且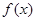 在
在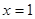 取得极大值2.
取得极大值2.
∴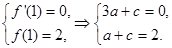 3分
3分
解得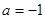 ,
,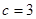 ,∴
,∴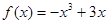 4分
4分
(2)∵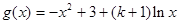 ,
,
∴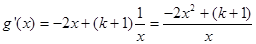 5分
5分
因为函数定义域为(0,+∞),所以
当k+1=0时,即k=-1 时, 
∴函数在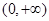 上单调递减 ;
6分
上单调递减 ;
6分
当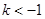 时 ,∵
时 ,∵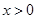
∴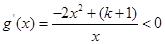
∴函数在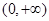 上单调递减
上单调递减
当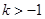 时,令
时,令 ,得
,得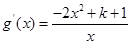 >0,∵
>0,∵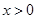
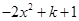 >0,得
>0,得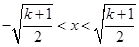
结合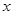 >0,
得0<
>0,
得0<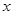 <
<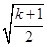 ,
,
令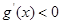 ,得
,得 <0,∴
<0,∴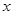 >
>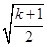 ,
,
函数在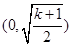 上单调递增,在
上单调递增,在 上单调递减。
9分
上单调递减。
9分
综上,当 时,函数的单调递减区间为
时,函数的单调递减区间为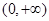 ,无单调递增区间;
,无单调递增区间;
当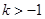 时,函数在
时,函数在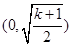 上单调递增,在
上单调递增,在 上单调递减。 10分
上单调递减。 10分
(3)当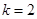 时,
时,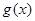 =
=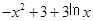 ,
,
令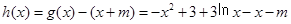
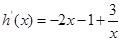 ,令
,令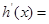 0,
0,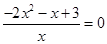 得
得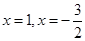 (舍去)
(舍去)
由函数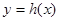 定义域为(0,+∞),
13分
定义域为(0,+∞),
13分
则当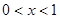 时,
时,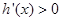 ,当
,当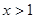 时
时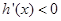 ,
,
∴当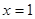 时,函数
时,函数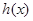 取得最小值1-
取得最小值1-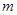 。
15分
。
15分
故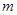 的取值范围是(1,+∞)。答
的取值范围是(1,+∞)。答
 也正确
16分
也正确
16分

 同步练习强化拓展系列答案
同步练习强化拓展系列答案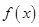 为奇函数,且当
为奇函数,且当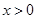 时,
时,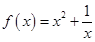 ,则
,则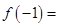 ( )
( )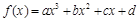 为奇函数,且在
为奇函数,且在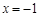 处取得极大值2.
处取得极大值2.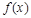 的解析式;
的解析式;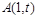 (
(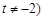 可作函数
可作函数 图像的三条切线,求实数
图像的三条切线,求实数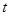 的取值范围;
的取值范围;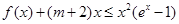 对于任意的
对于任意的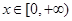 恒成立,求实数
恒成立,求实数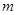 的取值范围.
的取值范围.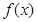 为奇函数,且
为奇函数,且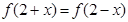 ,当
,当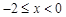 时,
时,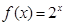 ,
,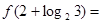 。
。 为奇函数,
为奇函数, 为偶函数,且
为偶函数,且 .
. ,则称
,则称 是函数
是函数