题目内容
已知函数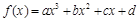 为奇函数,且在
为奇函数,且在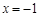 处取得极大值2.
处取得极大值2.
(Ⅰ)求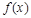 的解析式;
的解析式;
(Ⅱ)过点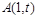 (
(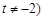 可作函数
可作函数 图像的三条切线,求实数
图像的三条切线,求实数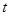 的取值范围;
的取值范围;
(Ⅲ)若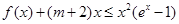 对于任意的
对于任意的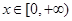 恒成立,求实数
恒成立,求实数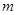 的取值范围.
的取值范围.
【答案】
(1)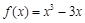 (2)
(2)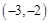 (3)
(3)
【解析】
试题分析:(I)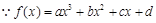 为奇函数
为奇函数
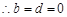
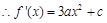
 在
在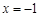 处取得极大值2
处取得极大值2
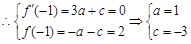
从而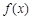 解析式为
解析式为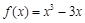 4分
4分
(2)设切点为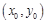 ,则
,则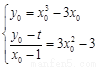
消去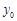 得
得
设 ,则
,则
 在
在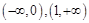 递减,
递减,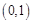 递增
递增
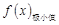
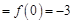 ,
,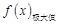 =
=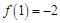
要使过点 可作函数
可作函数 图像的三条切线,则实数
图像的三条切线,则实数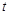 的取值范围为
的取值范围为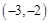
9分
(3)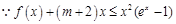
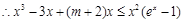 从而
从而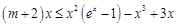
当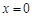 时,
时,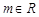
当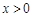 时,
时,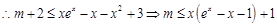
设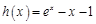
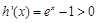
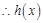 在
在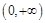 递增,
递增,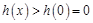
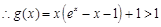
从而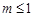
 实数
实数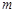 的取值范围为
的取值范围为 14分
14分
考点:导数的几何意义,导数的运用
点评:解决该试题的关键是对于导数几何意义以及导数的符号与函数单调性的关系的运用,属于基础题。

练习册系列答案
相关题目
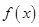 为奇函数,且当
为奇函数,且当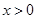 时,
时,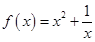 ,则
,则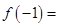 ( )
( ) 为奇函数,且
为奇函数,且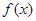 在
在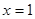 处取得极大值2.(1)求函数
处取得极大值2.(1)求函数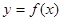 的解析式;
的解析式;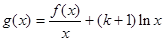 ,求函数
,求函数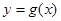 的单调区间;
的单调区间;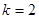 时,若函数
时,若函数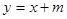 的下方,求
的下方,求 的取值范围。
的取值范围。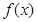 为奇函数,且
为奇函数,且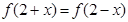 ,当
,当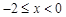 时,
时,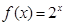 ,
,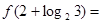 。
。 为奇函数,
为奇函数, 为偶函数,且
为偶函数,且 .
. ,则称
,则称 是函数
是函数