题目内容
已知P是双曲线
上的动点，F1、F2分别是双曲线的左、右焦点，M是∠F1PF2的平分线上的一点，且
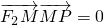，O为坐标原点，则|OM|=________．
3
分析：假设P在右支，延长F2M交PF1于点A，由题意：MF2垂直PM，故|AM|=|MF2|，|PA|=|PF2|，因为|PF1|-|PF2|=|PF1|-|PA|=|F1A|=2a=6，O为|F1F2|中点，M为|AF2|中点，由此能够求出|OM|的值．
解答：假设P在右支，
延长F2M交PF1于点A，
由题意：MF2垂直PM，
故|AM|=|MF2|，|PA|=|PF2|，
∵|PF1|-|PF2|=|PF1|-|PA|=|F1A|=2a=6，
O为|F1F2|中点，M为|AF2|中点，
∴|OM|=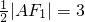
．
故答案为：3．
点评：本题考查双曲线的性质和应用，解题时要认真审题，仔细解答，注意公式的合理选用．
分析：假设P在右支，延长F2M交PF1于点A，由题意：MF2垂直PM，故|AM|=|MF2|，|PA|=|PF2|，因为|PF1|-|PF2|=|PF1|-|PA|=|F1A|=2a=6，O为|F1F2|中点，M为|AF2|中点，由此能够求出|OM|的值．
解答：假设P在右支，
延长F2M交PF1于点A，
由题意：MF2垂直PM，
故|AM|=|MF2|，|PA|=|PF2|，
∵|PF1|-|PF2|=|PF1|-|PA|=|F1A|=2a=6，
O为|F1F2|中点，M为|AF2|中点，
∴|OM|=
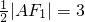．故答案为：3．
点评：本题考查双曲线的性质和应用，解题时要认真审题，仔细解答，注意公式的合理选用．
练习册系列答案
相关题目
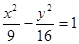上的动点，F1、F2分别是双曲线的左、右焦点，M是∠F1PF2的平分线上的一点，且
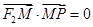，O为坐标原点，则|OM|= 
上的动点，F1、F2分别是其左、右焦点，O为坐标原点，则
的取值范围是
。
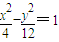上的动点，F1、F2分别是其左、右焦点，O为坐标原点，则
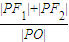的取值范围是 ．
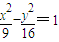上的动点，F1、F2分别是双曲线的左、右焦点，M是∠F1PF2的平分线上的一点，且
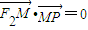，O为坐标原点，则|OM|= ．
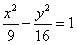上的动点，F1、F2分别是双曲线的左、右焦点，M是∠F1PF2的平分线上的一点，且
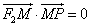，O为坐标原点，则|OM|=（ ）。