题目内容
已知P是双曲线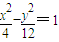 上的动点,F1、F2分别是其左、右焦点,O为坐标原点,则
上的动点,F1、F2分别是其左、右焦点,O为坐标原点,则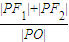 的取值范围是 .
的取值范围是 .
【答案】分析:设P(x,y) 则y2=3x2-12,e=2,由焦半径公式能够得出|PF1|=ex+a,|PF2|=ex-a,代入所求的式子并化简得到 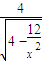 ,再由双曲线中x2≥4,求出范围即可.
,再由双曲线中x2≥4,求出范围即可.
解答:解答:解:设P(x,y) x>0,由焦半径公式|PF1|=ex+a,|PF2|=ex-a,
则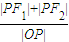 =
= (y2=3x2-12,e=2),
(y2=3x2-12,e=2),
则原式= =
=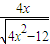 =
= ,又因为双曲线中x2≥4.
,又因为双曲线中x2≥4.
所以 ∈(2,4].
∈(2,4].
同理当x<0时,|PF1|=a-ex,|PF2|=-ex-a,
仍可推出 =
=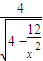 ∈(2,4].
∈(2,4].
即推出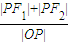 的取值范围为(2,4].
的取值范围为(2,4].
故答案为:(2,4].
点评:本题考查了双曲线的性质,由焦半径公式得到|PF1|=ex+a,|PF2|=ex-a是解题的关键,要注意分x>0和x<0两种情况作答,属于中档题.
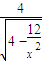 ,再由双曲线中x2≥4,求出范围即可.
,再由双曲线中x2≥4,求出范围即可.解答:解答:解:设P(x,y) x>0,由焦半径公式|PF1|=ex+a,|PF2|=ex-a,
则
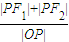 =
= (y2=3x2-12,e=2),
(y2=3x2-12,e=2),则原式=
 =
=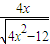 =
= ,又因为双曲线中x2≥4.
,又因为双曲线中x2≥4.所以
 ∈(2,4].
∈(2,4].同理当x<0时,|PF1|=a-ex,|PF2|=-ex-a,
仍可推出
 =
=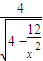 ∈(2,4].
∈(2,4].即推出
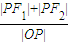 的取值范围为(2,4].
的取值范围为(2,4].故答案为:(2,4].
点评:本题考查了双曲线的性质,由焦半径公式得到|PF1|=ex+a,|PF2|=ex-a是解题的关键,要注意分x>0和x<0两种情况作答,属于中档题.

练习册系列答案
相关题目
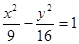 上的动点,F1、F2分别是双曲线的左、右焦点,M是∠F1PF2的平分线上的一点,且
上的动点,F1、F2分别是双曲线的左、右焦点,M是∠F1PF2的平分线上的一点,且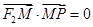 ,O为坐标原点,则|OM|=
,O为坐标原点,则|OM|=  上的动点,F1、F2分别是其左、右焦点,O为坐标原点,则
上的动点,F1、F2分别是其左、右焦点,O为坐标原点,则 的取值范围是
。
的取值范围是
。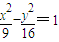 上的动点,F1、F2分别是双曲线的左、右焦点,M是∠F1PF2的平分线上的一点,且
上的动点,F1、F2分别是双曲线的左、右焦点,M是∠F1PF2的平分线上的一点,且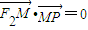 ,O为坐标原点,则|OM|= .
,O为坐标原点,则|OM|= .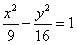 上的动点,F1、F2分别是双曲线的左、右焦点,M是∠F1PF2的平分线上的一点,且
上的动点,F1、F2分别是双曲线的左、右焦点,M是∠F1PF2的平分线上的一点,且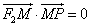 ,O为坐标原点,则|OM|=( )。
,O为坐标原点,则|OM|=( )。