题目内容
函数y=sinx,y=cosx在区间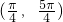 内围成图形的面积为
内围成图形的面积为
- A.

- B.

- C.

- D.

B
分析:根据定积分的几何意义,所求面积为S=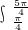 (sinx-cosx)dx,然后利用公式求出sinx-cosx的原函数F(x),算出F(
(sinx-cosx)dx,然后利用公式求出sinx-cosx的原函数F(x),算出F( )-F(
)-F( )的值,即为所求图形的面积.
)的值,即为所求图形的面积.
解答:根据题意,所求面积为
S=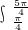 (sinx-cosx)dx=(-cosx-sinx+C)
(sinx-cosx)dx=(-cosx-sinx+C)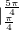 (其中C为常数)
(其中C为常数)
∴S=(-cos -sin
-sin +C)-(-cos
+C)-(-cos -sin
-sin +C)=(
+C)=( +
+ +C)-(-
+C)-(- -
- +C)=
+C)=
故选B
点评:本题以求两条三角函数图象所围成的面积为例,着重考查了定积分在求曲边图形的面积中的应用的知识点,属于基础题.
分析:根据定积分的几何意义,所求面积为S=
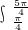 (sinx-cosx)dx,然后利用公式求出sinx-cosx的原函数F(x),算出F(
(sinx-cosx)dx,然后利用公式求出sinx-cosx的原函数F(x),算出F( )-F(
)-F( )的值,即为所求图形的面积.
)的值,即为所求图形的面积.解答:根据题意,所求面积为
S=
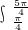 (sinx-cosx)dx=(-cosx-sinx+C)
(sinx-cosx)dx=(-cosx-sinx+C)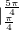 (其中C为常数)
(其中C为常数)∴S=(-cos
 -sin
-sin +C)-(-cos
+C)-(-cos -sin
-sin +C)=(
+C)=( +
+ +C)-(-
+C)-(- -
- +C)=
+C)=
故选B
点评:本题以求两条三角函数图象所围成的面积为例,着重考查了定积分在求曲边图形的面积中的应用的知识点,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,k∈z};
,k∈z}; 在[0,π]上是增函数.
在[0,π]上是增函数. 的图象向又平移
的图象向又平移 得到y=3sin2x的图象.
得到y=3sin2x的图象.