Question

已知函数f(x)=|1-|(x＞0)，

(1)当0＜a＜b,且f(a)=f(b)时，求证：ab＞1;

(2)是否存在实数a、b(a＜b),使得函数y=f(x)的定义域、值域都是［a,b］？若存在，则求出a、b的值；若不存在，请说明理由.

(3)若存在实数a、b(a＜b)，使得函数y=f(x)的定义域为［a,b］时，值域为［Ma,Mb］(M≠0),求M的取值范围.

Answer 1

(1)证明：∵x＞0,∴f(x)=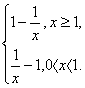                                                                    

∴f(x)在(0,1)上为减函数，在(1,+∞)上是增函数.??

由0＜a＜b,且f(a)=f(b),可得0＜a＜1＜b和-1=1-,即+=2.?

∴2AB=a+b＞2.                                                                                ?

故＞1,即AB＞1.                                                                               ?

(2)解：不存在满足条件的实数a、b.?

若存在满足条件的实数a、b，使得函数y=f(x)=|1-|的定义域、值域都是［a,b］，则a＞0，f(x)=

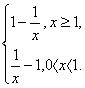
①当a、b∈(0,1)时，f(x)= -1在(0,1)上为减函数，故即?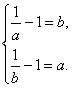

解得a=b.故此时不存在适合条件的实数a,b.                                              ?

②当a、b∈［1,+∞)时，f(x)=1-在(1,+∞)上是增函数，故即?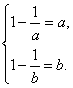

此时a、b是方程x²-x+1=0的根，此方程无实根.??

故此时不存在适合条件的实数a、b.                                                         

当a∈(0,1),b∈［1,+∞)时，由于1∈［a,b］，而f(1)=0［a,b］,故此时不存在适合条件的实数a、b.?

综上，可知不存在适合条件的实数a、b.                                                  

(3)解：若存在实数a、b(a＜b),使得函数y=f(x)的定义域为［a,b］时值域为［ma,mb］，则a＞0,m＞0.??

①当a、b∈(0,1)时，由于f(x)在(0,1)上是减函数，值域为［ma,mb］，即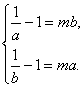

此时a,b异号，不合题意，所以a,b不存在.?

②当a∈(0,1)或b∈(1,+∞)时，由(2)知0在值域内，值域不可能是［ma,mb］，所以a、b不存在.故只有a、b∈［1,+∞).?

∵f(x)=|1-|在(1,+∞)上是增函数,∴即?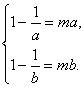

a、b是方程mx²-x+1=0的两个根，?

即关于x的方程mx²-x+1=0有两个大于1的实根.                                              ?

设这两个根为x₁、x₂,则x₁+x₂=,x_1·x₂=.??

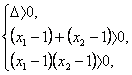∴即?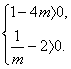

解之，得0＜m＜.?

故m的取值范围是0＜m＜.