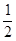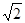题目内容
(本小题14分)
已知等比数列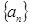 满足
满足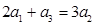 ,且
,且 是
是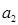 ,
,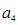 的等差中项.
的等差中项.
(Ⅰ)求数列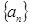 的通项公式;
的通项公式;
(Ⅱ)若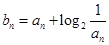 ,
,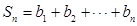 ,求使
,求使  成立的正整数
成立的正整数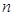 的最小值.
的最小值.
已知等比数列
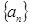 满足
满足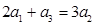 ,且
,且 是
是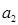 ,
,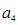 的等差中项.
的等差中项.(Ⅰ)求数列
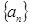 的通项公式;
的通项公式;(Ⅱ)若
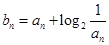 ,
,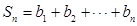 ,求使
,求使  成立的正整数
成立的正整数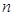 的最小值.
的最小值.(1)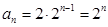 (2)使
(2)使 成立的正整数
成立的正整数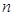 的最小值为10
的最小值为10
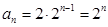 (2)使
(2)使 成立的正整数
成立的正整数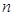 的最小值为10
的最小值为10试题分析:解:(Ⅰ)设等比数列
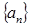 的首项为
的首项为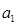 ,公比为
,公比为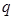 ,
,依题意,有
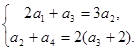 即
即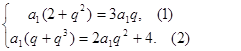
由
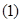 得
得 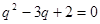 ,解得
,解得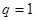 或
或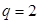 .
.当
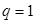 时,不合题意舍;
时,不合题意舍;当
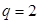 时,代入(2)得
时,代入(2)得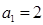 ,所以,
,所以,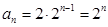 .
. (Ⅱ)
 .
. 所以

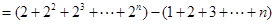

因为
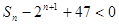 ,所以
,所以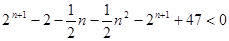 ,
,即
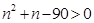 ,解得
,解得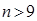 或
或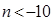 .
. 因为
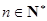 ,故使
,故使 成立的正整数
成立的正整数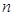 的最小值为10 .
的最小值为10 . 点评:解决该试题的关键是对于等差数列和等比数列的通项公式和性质的熟练运用,以及分组求和,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,则
,则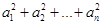 等于( )
等于( )
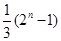
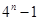
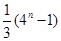
 ,周三、周四两天,每天上涨
,周三、周四两天,每天上涨
 ,末项为
,末项为 ,其中任意连续三项a,b,c满足b=
,其中任意连续三项a,b,c满足b= ,则此数列的第15项是 .
,则此数列的第15项是 . ,且
,且 是
是 和
和 的等比中项,则动点
的等比中项,则动点 的轨迹为除去
的轨迹为除去 轴上点的( )
轴上点的( )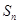 是数列{
是数列{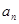 }的前n项和,
}的前n项和, ,那么数列{
,那么数列{ 中, 若
中, 若 是方程
是方程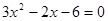 的两根,则
的两根,则 =___________.
=___________.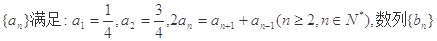 满足:
满足: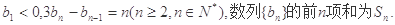
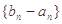 为等比数列;
为等比数列;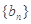 为递增数列;
为递增数列; 的取值范围。
的取值范围。 的公比为正数,且
的公比为正数,且 ,
, ,则
,则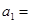 ( )
( )