题目内容
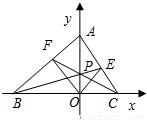
如图,在平面直角坐标系xoy中,设三角形ABC的顶点分别为A(0,a),B(b,0),C(c,0),点P(0,p)在线段AO上的一点(异于端点),这里a,b,c,p均为非零实数,设直线BP,CP分别与边AC,AB交于点E,F.(1)若BE⊥AC,求证CF⊥AB;
(2)若O、E分别是BC、AC的中点,求证F也是AB的中点.
【答案】分析:(1)根据B和P的坐标求出直线BP的斜率,同理根据A和C的坐标求出直线AC的斜率,因为两直线垂直得到斜率乘积为-1,令两斜率相乘等于-1得到一个关系式pa=-bc;然后根据P和C的坐标求出直线PC 的斜率,根据A和B的坐标求出直线AB的斜率,把两斜率相乘后,把求得的关系式代入即可得到乘积为-1,得到CF垂直于AB,得证;
(2)由O是BC的中点且PO垂直于BC,得到直线PO为线段BC的垂直平分线,根据线段垂直平分线的性质可知:|PB|=|PC|,且|AB|=|AC|,根据等边对等角得到角PBC等于角PCB,且角ABC等于角ACB,两等式相减得到角ABP等于角ACF,又根据对顶角相等得到三角形PFB与三角形PEC全等,得到|FB|等于|EC|,所以得到|FB|等于|AB|的一半,得证.
解答:证明:(1)根据点B(b,0)和点P的坐标(0,p)写出直线BP的斜率为-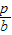 ,
,
由点A(0,a)和C(c,0)写出直线AC的斜率为- ,
,
因为BE⊥AC,所以(-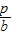 )(-
)(-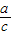 )=-1,即pa=-bc;
)=-1,即pa=-bc;
而由C(c,0)和P(0,p)斜率为- ,由A(0,a)和B(b,0)斜率为-
,由A(0,a)和B(b,0)斜率为-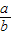 ,
,
则斜率之积为(-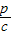 )(-
)(-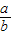 )=
)=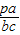 =
=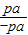 =-1,所以CF⊥AB;
=-1,所以CF⊥AB;
(2)因为O为线段BC的中点,且PO⊥BC,所以OP为线段BC的垂直平分线,
∴|BP|=|CP|,且|AB|=|AC|,
∴∠PBO=∠PCO,且∠ABC=∠ACB,
∴∠ABP=∠ACP,
又∠FPB=∠EPC,
∴△BPF≌△CPE,
∴|BF|=|CE|,
又E是线段AC的中点,所以|CE|= |AC|,
|AC|,
则|BF|= |AB|,所以F为线段AB的中点.
|AB|,所以F为线段AB的中点.
点评:此题考查学生掌握两直线垂直时斜率所满足的关系以及会根据斜率乘积为-1得到两直线垂直,灵活运用线段垂直平分线的性质及三角形全等解决实际问题,是一道综合题.
(2)由O是BC的中点且PO垂直于BC,得到直线PO为线段BC的垂直平分线,根据线段垂直平分线的性质可知:|PB|=|PC|,且|AB|=|AC|,根据等边对等角得到角PBC等于角PCB,且角ABC等于角ACB,两等式相减得到角ABP等于角ACF,又根据对顶角相等得到三角形PFB与三角形PEC全等,得到|FB|等于|EC|,所以得到|FB|等于|AB|的一半,得证.
解答:证明:(1)根据点B(b,0)和点P的坐标(0,p)写出直线BP的斜率为-
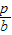 ,
,由点A(0,a)和C(c,0)写出直线AC的斜率为-
 ,
,因为BE⊥AC,所以(-
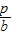 )(-
)(-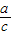 )=-1,即pa=-bc;
)=-1,即pa=-bc;而由C(c,0)和P(0,p)斜率为-
 ,由A(0,a)和B(b,0)斜率为-
,由A(0,a)和B(b,0)斜率为-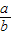 ,
,则斜率之积为(-
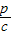 )(-
)(-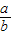 )=
)=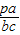 =
=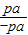 =-1,所以CF⊥AB;
=-1,所以CF⊥AB;(2)因为O为线段BC的中点,且PO⊥BC,所以OP为线段BC的垂直平分线,
∴|BP|=|CP|,且|AB|=|AC|,
∴∠PBO=∠PCO,且∠ABC=∠ACB,
∴∠ABP=∠ACP,
又∠FPB=∠EPC,
∴△BPF≌△CPE,
∴|BF|=|CE|,
又E是线段AC的中点,所以|CE|=
 |AC|,
|AC|,则|BF|=
 |AB|,所以F为线段AB的中点.
|AB|,所以F为线段AB的中点.点评:此题考查学生掌握两直线垂直时斜率所满足的关系以及会根据斜率乘积为-1得到两直线垂直,灵活运用线段垂直平分线的性质及三角形全等解决实际问题,是一道综合题.

练习册系列答案
相关题目
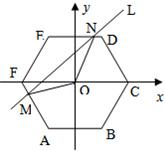 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
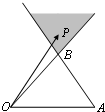 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是