��Ŀ����
��֪f��ֱ������ƽ��xOy��������һ��ӳ�䣬��P��ӳ��f�µ���Ϊ��Q������Q=f��P������P1��x1��y1����P2=f��P1����P3=f��P2��������Pn=f��Pn-1���������������һ��Բ��ʹ���еĵ�Pn��xn��yn����n��N*���������Բ�ڻ�Բ�ϣ���ô�����ԲΪ��Pn��xn��yn����һ������Բ���ر�أ���P1=f��P1��ʱ����Ƶ�P1Ϊӳ��f�µIJ����㣮
���� ����P��x��y����ӳ��f�µ���Ϊ��Q��2x��1-y����
����ӳ��f�²���������ꣻ
����P1������Ϊ��1��2�����жϵ�Pn��xn��yn����n��N*���Ƿ����һ���뾶Ϊ3������Բ����˵�����ɣ�
���� ����P��x��y����ӳ��f�µ���Ϊ��Q(
| x+y |
| 2 |
| x-y |
| 2 |
| 5 |
�����������費���������ΪP0��x0��y0�������ݶ�Ӧ��ϵ��������Ķ��壬�нⷽ����
�����⼴�ɣ�
����P1��1��2������P2��2��-1����P3��4��2����P4��8��-1������|P1P4|=
��6�����P1��P4��������ͬ һ���뾶Ϊ3��Բ��
���� ��Pn+1=f��Pn�����ã�
���������ȱ����� д�����ǵ�ͨ�ʽ����A��3��1����������Pn��A�ľ��룬�ɵô˾���С��
�������еĵ�Pn��n��N*�������� PΪԲ�ģ�
Ϊ�뾶��Բ�ڣ�
|
����P1��1��2������P2��2��-1����P3��4��2����P4��8��-1������|P1P4|=
| 58 |
���� ��Pn+1=f��Pn�����ã�
|
| 5 |
| 5 |
����⣺���ٽ⣺�費���������ΪP0��x0��y0����
�����⣬��
�����x0=0�� y0=
��
����ӳ��f�²�����ΪP0(0��
)
�ڽ��ۣ���Pn��xn��yn��������һ���뾶Ϊ3������Բ��
֤������P1��1��2������P2��2��-1����P3��4��2����P4��8��-1����
����|P1P4|=
��6��
���P1��P4��������ͬ һ���뾶Ϊ3��Բ�ڣ�
���Ե�Pn��xn��yn����n��N*�� ������һ���뾶Ϊ3������Բ
����֤������P1��2��3������P2(
��-
)��
��Pn+1=f��Pn������
����xn+1+yn+1=xn+1��xn+1-yn+1=yn+1��
��Pn+2=f��Pn+1������
��
����xn+2=
xn+
�� yn+2=
yn+
��xn+2-3=
(xn-3)�� yn+2-1=
(yn-1)��
��x1-3��0��x2-3��0����xn-3��0��
ͬ��yn-1��0��
����
=
��
=
��
��������{x2n-1-3}��{x2n-3}��n��N*�����ǹ���Ϊ
�ĵȱ����У�����ֱ�Ϊ x1-3=-1�� x2-3=
��
����x2n-1-3=-(
)n-1�� x2n-3=
��(
)n-1��
ͬ���ɵ�y2n-1-1=2��(
)n-1�� y2n-1=-
��(
)n-1
���Զ�����n��N*��|xn-3|��1��|yn-1|��2��
��A��3��1������|APn|=
��
��
����|APn|��
��
�����еĵ�Pn��n��N*��������A��3��1��ΪԲ�ģ�
Ϊ�뾶��Բ�ڻ�Բ�ϣ�
����Pn��xn��yn������һ���뾶Ϊ
������Բ
�����⣬��
|
| 1 |
| 2 |
����ӳ��f�²�����ΪP0(0��
| 1 |
| 2 |
�ڽ��ۣ���Pn��xn��yn��������һ���뾶Ϊ3������Բ��
֤������P1��1��2������P2��2��-1����P3��4��2����P4��8��-1����
����|P1P4|=
| 58 |
���P1��P4��������ͬ һ���뾶Ϊ3��Բ�ڣ�
���Ե�Pn��xn��yn����n��N*�� ������һ���뾶Ϊ3������Բ
����֤������P1��2��3������P2(
| 7 |
| 2 |
| 1 |
| 2 |
��Pn+1=f��Pn������
|
����xn+1+yn+1=xn+1��xn+1-yn+1=yn+1��
��Pn+2=f��Pn+1������
|
����xn+2=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��xn+2-3=
| 1 |
| 2 |
| 1 |
| 2 |
��x1-3��0��x2-3��0����xn-3��0��
ͬ��yn-1��0��
����
| xn+2-3 |
| xn-3 |
| 1 |
| 2 |
| yn+2-1 |
| yn-1 |
| 1 |
| 2 |
��������{x2n-1-3}��{x2n-3}��n��N*�����ǹ���Ϊ
| 1 |
| 2 |
| 1 |
| 2 |
����x2n-1-3=-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
ͬ���ɵ�y2n-1-1=2��(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
���Զ�����n��N*��|xn-3|��1��|yn-1|��2��
��A��3��1������|APn|=
| (xn-3)2+(yn-1)2 |
| 1+4 |
����|APn|��
| 5 |
�����еĵ�Pn��n��N*��������A��3��1��ΪԲ�ģ�
| 5 |
����Pn��xn��yn������һ���뾶Ϊ
| 5 |
���������⿼��ӳ��Ķ��壬����ȱ����в���ͨ�ʽ�������ľ��빫ʽ��Ӧ�ã��������������⣬�Ķ�������Ϣ��������

��ϰ��ϵ�д�
 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д�
�����Ŀ
 ��P1(2��3)����֤����Pn(xn��yn)(n��N*)����һ���뾶Ϊ
��P1(2��3)����֤����Pn(xn��yn)(n��N*)����һ���뾶Ϊ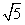 ������Բ��
������Բ��