题目内容
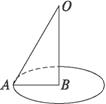
10、过半径为2的球O表面上一点A作球O的截面，若OA与该截面所成的角是60°，则该截面的面积是
π
．分析：充分利用球的半径OA、球心与截面圆心的连线、OA在截面圆上的射影构成的直角三角形解决即可．
解答：解：设截面的圆心为Q，
由题意得：∠OAQ=60°，QA=1，
∴S=π•12=π．
答案：π．
由题意得：∠OAQ=60°，QA=1，
∴S=π•12=π．
答案：π．
点评：本题主要考查了球的性质、直线与平面所成的角，还考查了空间想象力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
过半径为2的球O表面上一点A作球O的截面，若OA与该截面所成的角是60°则该截面的面积是（ ）
| A、π | ||
| B、2π | ||
C、2
| ||
| D、3π |
π
