题目内容
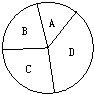
 28、现有5种不同颜色的染料,要对如图中的四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色,则不同的着色方法的种数是
28、现有5种不同颜色的染料,要对如图中的四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色,则不同的着色方法的种数是
260
(用数字作答).分析:首先分析题目求5种不同颜色,对四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色的着色种数,故可以根据使用颜色的多少分情况讨论.情况1:用到4种颜色,情况2:用到3种颜色,情况3:用到2中颜色,分别求出它们的种数相加即可得到答案.
解答:解,情况1:用到4种颜色:C54•A44=24×5=120
情况2:用到3种颜色即AC或BD有一对同色:2×C53A33=120
情况3:用到2中颜色即AC同色,BD也同色:C52×A23=20
故有120+120+20=260种着色的方法.
故答案为260.
情况2:用到3种颜色即AC或BD有一对同色:2×C53A33=120
情况3:用到2中颜色即AC同色,BD也同色:C52×A23=20
故有120+120+20=260种着色的方法.
故答案为260.
点评:此题主要考查排列组合及简单的计数原理在实际中的应用问题,对于此类对图形着色问题,在近几年的高考中多次出现,同学们需要很好的掌握做题方法.

练习册系列答案
相关题目
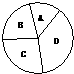 7、现有5种不同颜色的染料,要对如图中的四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色,则不同的着色方法的种数是( )
7、现有5种不同颜色的染料,要对如图中的四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色,则不同的着色方法的种数是( )