题目内容
已知函数 ,数列
,数列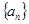 满足
满足
(I)求证:数列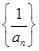 是等差数列;
是等差数列;
(II)令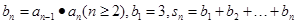 ,若
,若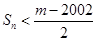 对一切
对一切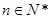 成立,求最小正整数
成立,求最小正整数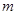 .
.
【答案】
(1)证明:由题意可得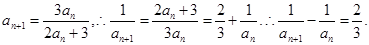
又 数列
数列 是以
是以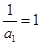 为首项,以
为首项,以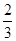 为公差的等差数列.
为公差的等差数列.
(2)由(1)可得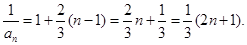
 当
当 时,
时,
当 时,上式同样成立。[来源:Z§xx§k.Com]
时,上式同样成立。[来源:Z§xx§k.Com]
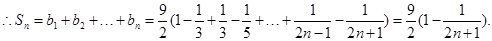
 即
即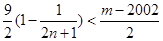 对一切
对一切 成立,
成立,
又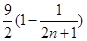 随
随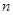 递增,且
递增,且

【解析】略

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 ,数列{
,数列{ }满足
}满足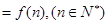 ,且{
,且{ 的取值范围是 ( )
的取值范围是 ( ) B.
B. 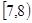 C.
C.  D.
D. 
 ,数列
,数列 满足
满足 ,
,
 ;
;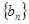 满足
满足 …+
…+ ,求
,求
 ,数列
,数列 满足
满足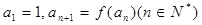
 求数列
求数列 ,求
,求 .
. ,数列
,数列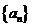 满足
满足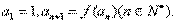
 ,求
,求 .
. ,数列
,数列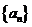 满足
满足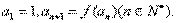
 ,求
,求 .
.