题目内容
下列四个命题：
（1）函数f（x）在x≥0时是增函数，x≤0也是增函数，所以f（x）在R上是增函数；
（2）若二次函数f（x）=ax2+bx+2没有零点，则b2-8a＜0且a≠0；
（3） y=x2-2|x|-3的递增区间为[1，+∞）；
（4） 若f（-2）=f（2），则定义在R上的函数f（x）不是奇函数．其中正确的命题是 ________．
解：对于（3），因为 y=x2-2|x|-3是偶函数，其定义域关于原点对称，其单调区间也关于原点对称，所以递增区间应有两个，是[1，+∞）和（-∞，-1]，故（3）错
对于（4），取f（x）=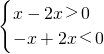
，满足f（-2）=f（2），但f（x）是奇函数，故（4）错
故答案为：（1）（2）
分析：本题是多选题，可采用逐一检验的方法，对于错的③和④采用举出反例或找出矛盾就能说明其不正确．
点评：这是函数方面的一道综合题，考查了函数的单调性，奇偶性，零点的存在性，是基础题
对于（4），取f（x）=
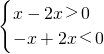，满足f（-2）=f（2），但f（x）是奇函数，故（4）错故答案为：（1）（2）
分析：本题是多选题，可采用逐一检验的方法，对于错的③和④采用举出反例或找出矛盾就能说明其不正确．
点评：这是函数方面的一道综合题，考查了函数的单调性，奇偶性，零点的存在性，是基础题
练习册系列答案
相关题目