题目内容
已知及是实数集,e是自然对数的底数,函数f(x)=| 1+In(x+1) |
| x |
(I)解关于x的不等式f(x2+1)>
| 2 |
| e-1 |
(II)若常数k是正整数,当x>0时,f(x)>
| k |
| x+1 |
分析:(I)看出要解的不等式右边可以写成f(e-1),问题转化为抽象函数的不等式的问题,对函数求导判断函数的单调性,根据函数的单调性写出解题的不等式,得到解集.
(II)利用特值看出要求的最大值是3,后面要证明当取3时,式子恒成立,利用导数求出函数的单调区间,看出函数在当x=e-1时,g(x)取得最小值g(e-1)=3-e,得到结论.
(II)利用特值看出要求的最大值是3,后面要证明当取3时,式子恒成立,利用导数求出函数的单调区间,看出函数在当x=e-1时,g(x)取得最小值g(e-1)=3-e,得到结论.
解答:解:(I)∵f(e-1)=
∴不等式f(x2+1)>
可以化为f(x2+1)>f(e-1)
∴f′(x)=
[
-1-ln(x+1)]=-
[
+ln(x+1)]
∴当x>0时,f′(x)<0,
∴函数f(x)在区间(0,+∞)上是减函数,
∵f(x2+1)>f(e-1),
∴x2+1<e-1,
∴-
<x<
,
∴不等式的解集是{x|-
<x<
}
(II)∵当x>0时,f(x)>
恒成立,
令x=1,得k<2(1+ln2)
∵k是整数,
∴k=3.
下面证明当k=3,x>0时,f(x)>
恒成立,
即当x>0时,(x+1)ln(x+1)+1-2x>0恒成立,
令g(x)=(x+1)ln(x+1)+1-2x
则g′(x)=ln(x+1)-1
当x>e-1时,g′(x)>0,
当0<x<e-1时,g′(x)<0
∴当x=e-1时,g(x)取得最小值g(e-1)=3-e>0
∴当x>0时,(x+1)ln(x+1)+1-2x>0恒成立,
∴正整数k的最大值是3.
| 2 |
| e-1 |
∴不等式f(x2+1)>
| 2 |
| e-1 |
∴f′(x)=
| 1 |
| x2 |
| x |
| x+1 |
| 1 |
| x2 |
| 1 |
| x+1 |
∴当x>0时,f′(x)<0,
∴函数f(x)在区间(0,+∞)上是减函数,
∵f(x2+1)>f(e-1),
∴x2+1<e-1,
∴-
| e-2 |
| e-2 |
∴不等式的解集是{x|-
| e-2 |
| e-2 |
(II)∵当x>0时,f(x)>
| k |
| x+1 |
令x=1,得k<2(1+ln2)
∵k是整数,
∴k=3.
下面证明当k=3,x>0时,f(x)>
| k |
| x+1 |
即当x>0时,(x+1)ln(x+1)+1-2x>0恒成立,
令g(x)=(x+1)ln(x+1)+1-2x
则g′(x)=ln(x+1)-1
当x>e-1时,g′(x)>0,
当0<x<e-1时,g′(x)<0
∴当x=e-1时,g(x)取得最小值g(e-1)=3-e>0
∴当x>0时,(x+1)ln(x+1)+1-2x>0恒成立,
∴正整数k的最大值是3.
点评:本题考查函数的综合问题,涉及到的知识点比较全面,是可以作为压轴题目的一个解答题,特别的题目应用到函数的恒成立问题,这是每一年必考的知识点.

练习册系列答案
相关题目
 在A,B,C,D四小题中只能选做2题,每题10分,共计20分.
在A,B,C,D四小题中只能选做2题,每题10分,共计20分. 的定义域为{x|x>0,x∈R}
的定义域为{x|x>0,x∈R} :
: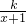 恒成立,求k的最大值.
恒成立,求k的最大值. 的定义域为{x|x>0,x∈R}
的定义域为{x|x>0,x∈R} :
: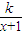 恒成立,求k的最大值.
恒成立,求k的最大值.