题目内容
一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从袋中拿一个球(拿后放回),记下标号.若拿出球的标号是3的倍数,则得1分,否则得-1分.
(1)求拿4次至少得2分的概率;
(2)求拿4次所得分数ξ的分布列和数学期望.
解:(1)设拿出球的号码是3的倍数的为事件A,则P(A)= ,
,
拿4次至少得2分包括2分和4分两种情况.
 =
=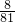 ,
,
P=P1+P2= …(5分)
…(5分)
(2)ξ的可能取值为-4,-2,0,2,4,
则P(ξ=-4)=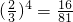 ; P(ξ=-2)=
; P(ξ=-2)=
P(ξ=0)=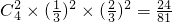 P( ξ=2)=
P( ξ=2)=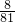 ,P( ξ=4)=
,P( ξ=4)=
∴分布列为
∴Eξ=-4×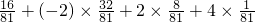 =-
=- …(14分)
…(14分)
分析:(1)拿4次至少得2分包括2分和4分两种情况,这两种情况是互斥的,根据独立重复试验的概率公式做出结果,再把两部分相加得到结果.
(2)看出变量的可能的取值,结合变量对应的事件,做出变量对应的概率和分布列,再做出变量对应的期望值.
点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是利用独立重复试验的概率公式做出概率的值,本题是一个中档题目.
 ,
,拿4次至少得2分包括2分和4分两种情况.
 =
=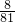 ,
,
P=P1+P2=
 …(5分)
…(5分)(2)ξ的可能取值为-4,-2,0,2,4,
则P(ξ=-4)=
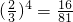 ; P(ξ=-2)=
; P(ξ=-2)=
P(ξ=0)=
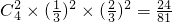 P( ξ=2)=
P( ξ=2)=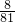 ,P( ξ=4)=
,P( ξ=4)=
∴分布列为
| P | -4 | -2 | 0 | 2 | 4 |
| ξ | 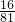 |  | 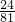 | 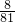 |  |
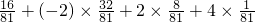 =-
=- …(14分)
…(14分)分析:(1)拿4次至少得2分包括2分和4分两种情况,这两种情况是互斥的,根据独立重复试验的概率公式做出结果,再把两部分相加得到结果.
(2)看出变量的可能的取值,结合变量对应的事件,做出变量对应的概率和分布列,再做出变量对应的期望值.
点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是利用独立重复试验的概率公式做出概率的值,本题是一个中档题目.

练习册系列答案
相关题目