题目内容
已知双曲线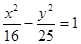 的左焦点为
的左焦点为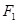 ,点
,点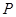 为双曲线右支上一点,且
为双曲线右支上一点,且 与圆
与圆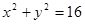 相切于点
相切于点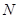 ,
,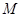 为线段
为线段 的中点,
的中点,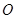 为坐标原点, 则
为坐标原点, 则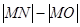 =
=
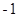
解析试题分析:设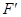 是双曲线的右焦点,连接
是双曲线的右焦点,连接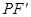 ,因为
,因为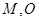 分别是
分别是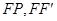 的中点,所以
的中点,所以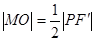 ,所以
,所以 ,由双曲线的定义知,
,由双曲线的定义知,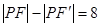 ,故
,故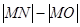
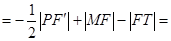
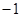 .
.
考点:圆与圆锥曲线的综合;直线与圆的位置关系.
点评:本题考查圆与双曲线的综合,解题的关键是正确运用双曲线的定义,三角形的中位线性质.

练习册系列答案
相关题目
题目内容
已知双曲线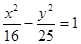 的左焦点为
的左焦点为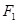 ,点
,点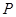 为双曲线右支上一点,且
为双曲线右支上一点,且 与圆
与圆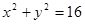 相切于点
相切于点 ,
, 为线段
为线段 的中点,
的中点,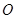 为坐标原点, 则
为坐标原点, 则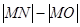 =
=
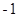
解析试题分析:设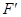 是双曲线的右焦点,连接
是双曲线的右焦点,连接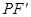 ,因为
,因为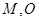 分别是
分别是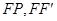 的中点,所以
的中点,所以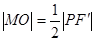 ,所以
,所以 ,由双曲线的定义知,
,由双曲线的定义知,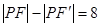 ,故
,故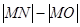
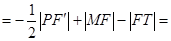
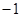 .
.
考点:圆与圆锥曲线的综合;直线与圆的位置关系.
点评:本题考查圆与双曲线的综合,解题的关键是正确运用双曲线的定义,三角形的中位线性质.
