题目内容
对于定义域分别为M,N的函数y=f(x),y=g(x),规定:函数h(x)=
|
(1)若函数f(x)=
| 1 |
| x+1 |
(2)若g(x)=f(x+α),其中α是常数,且α∈[0,2π],请问,是否存在一个定义域为R的函数y=f(x)及一个α的值,使得h(x)=cosx,若存在请写出一个f(x)的解析式及一个α的值,若不存在请说明理由.
分析:(1)先根据函数定义域的求法求出M,N,即可得到函数h(x)的解析式,再结合基本不等式进而求出函数h(x)的取值集合;
(2)先根据函数y=f(x)的定义域为R,得g(x)=f(x+a)的定义域为R;再结合函数h(x)的表达式得到cosx=f(x)•f(x+a);然后可以将cosx分解成两个函数的乘积,而且这两个函数还可以通过平移相互转化.
(2)先根据函数y=f(x)的定义域为R,得g(x)=f(x+a)的定义域为R;再结合函数h(x)的表达式得到cosx=f(x)•f(x+a);然后可以将cosx分解成两个函数的乘积,而且这两个函数还可以通过平移相互转化.
解答:解(1)由函数f(x)=
,g(x)=x2+2x+2,x∈R可得M={x|x≠-1},N=R
从而h(x)=
…..(2分)
当x>-1时,h(x)=
=
=x+1+
≥2….(4分)
当x<-1时,h(x)=
=
=-(-x-1+
)≤-2….(6分)
所以h(x)的取值集合为{y|y≤-2,或y≥2或y=1}….(7分)
(2)由函数y=f(x)的定义域为R,得g(x)=f(x+a)的定义域为R
所以,对于任意x∈R,都有h(x)=f(x)•g(x)即对于任意x∈R,都有cosx=f(x)•f(x+a)
所以,我们考虑将cosx分解成两个函数的乘积,而且这两个函数还可以通过平移相互转化cosx=cos2
-sin2
=(cos
+sin
)(cos
-sin
)=
cos(
-
)•
cos(
+
)
所以,令f(x)=
cos(
-
),且α=π,即可 …..(14分)
又cosx=1-2sin2
=(1+
sin
)(1-
sin
)
所以,令f(x)=1+
sin
,且α=2π,即可(答案不唯一)
| 1 |
| x+1 |
从而h(x)=
|
当x>-1时,h(x)=
| x2+2x+2 |
| x+1 |
| (x+1)2+1 |
| x+1 |
| 1 |
| x+1 |
当x<-1时,h(x)=
| x2+2x+2 |
| x+1 |
| (x+1)2+1 |
| x+1 |
| 1 |
| -x-1 |
所以h(x)的取值集合为{y|y≤-2,或y≥2或y=1}….(7分)
(2)由函数y=f(x)的定义域为R,得g(x)=f(x+a)的定义域为R
所以,对于任意x∈R,都有h(x)=f(x)•g(x)即对于任意x∈R,都有cosx=f(x)•f(x+a)
所以,我们考虑将cosx分解成两个函数的乘积,而且这两个函数还可以通过平移相互转化cosx=cos2
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 2 |
| x |
| 2 |
| π |
| 4 |
| 2 |
| x |
| 2 |
| π |
| 4 |
所以,令f(x)=
| 2 |
| x |
| 2 |
| π |
| 4 |
又cosx=1-2sin2
| x |
| 2 |
| 2 |
| x |
| 2 |
| 2 |
| x |
| 2 |
所以,令f(x)=1+
| 2 |
| x |
| 2 |
点评:本题主要考查分段函数的解析式求法及其图象的作法以及函数的值域的求法.分段函数的值域是先分段求出,最后再综合.

练习册系列答案
相关题目
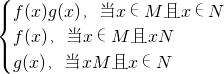
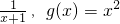 +2x+2,x∈R,求函数h(x)的取值集合;
+2x+2,x∈R,求函数h(x)的取值集合;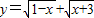 的最大值和最小值分别为M和m,则
的最大值和最小值分别为M和m,则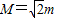 ;
;