题目内容
(理)已知向量 ,
, (n为正整数),函数
(n为正整数),函数 ,设f(x)在(0,+∞)上取最小值时的自变量x取值为an.
,设f(x)在(0,+∞)上取最小值时的自变量x取值为an.(1)求数列{an}的通项公式;
(2)已知数列{bn},对任意正整数n,都有bn•(4an2-5)=1成立,设Sn为数列{bn}的前n项和,求
 ;
;(3)在点列A1(1,a1)、A2(2,a2)、A3(3,a3)、…、An(n,an)、…中是否存在两点Ai,Aj(i,j为正整数)使直线AiAj的斜率为1?若存在,则求出所有的数对(i,j);若不存在,请你写出理由.
【答案】分析:(1)根据平面向量数量积的坐标公式,代入得f(x)= 是一个关于x二次函数,其图象是开口向上抛物线,在对称轴处函数取到最小值,由二次函数对称轴方程,得到数列{an}的通项公式;
是一个关于x二次函数,其图象是开口向上抛物线,在对称轴处函数取到最小值,由二次函数对称轴方程,得到数列{an}的通项公式;
(2)根据(1)的结论,将 代入bn的表达式,得到
代入bn的表达式,得到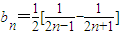 ,用裂项的方法求出其前n项和Sn的表达式,最后可得其极限
,用裂项的方法求出其前n项和Sn的表达式,最后可得其极限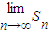 的值;
的值;
(3)对于这类问题,我们可以先假设存在满足条件的数对(i,j),然后再进行推理可得结论.具体作法:任取Ai、Aj(i、j∈N*,i≠j),设AiAj 所在直线的斜率为kij,则 ,从而得到不存在满足条件的数对(i,j),得出结论.
,从而得到不存在满足条件的数对(i,j),得出结论.
解答:解:(1)f(x)= …(2分)
…(2分)
函数y=f(x)的图象是一条抛物线,抛物线的顶点横坐标为 ,
,
开口向上,在(0,+∞) 上,当 时函数取得最小值,
时函数取得最小值,
所以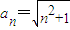 ;…(4分)
;…(4分)
(2)将(1)中{an}的表达式代入,得 .…(6分)
.…(6分)
∴ ,…(8分)
,…(8分)
所以所求的极限为: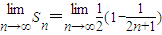 =
= ;…(10分)
;…(10分)
(3)任取Ai、Aj(i、j∈N*,i≠j),设AiAj 所在直线的斜率为kij,
则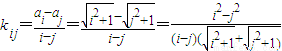 =
= .
.
因此不存在满足条件的数对(i,j),使直线AiAj的斜率为1.…(16分)
点评:本题综合了数列与向量、数列与函数以及数列的极限等知识点,是一道难题.对思维的要求较高,考查了转化化归和函数与方程的数学思想.
 是一个关于x二次函数,其图象是开口向上抛物线,在对称轴处函数取到最小值,由二次函数对称轴方程,得到数列{an}的通项公式;
是一个关于x二次函数,其图象是开口向上抛物线,在对称轴处函数取到最小值,由二次函数对称轴方程,得到数列{an}的通项公式;(2)根据(1)的结论,将
 代入bn的表达式,得到
代入bn的表达式,得到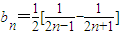 ,用裂项的方法求出其前n项和Sn的表达式,最后可得其极限
,用裂项的方法求出其前n项和Sn的表达式,最后可得其极限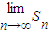 的值;
的值;(3)对于这类问题,我们可以先假设存在满足条件的数对(i,j),然后再进行推理可得结论.具体作法:任取Ai、Aj(i、j∈N*,i≠j),设AiAj 所在直线的斜率为kij,则
 ,从而得到不存在满足条件的数对(i,j),得出结论.
,从而得到不存在满足条件的数对(i,j),得出结论.解答:解:(1)f(x)=
 …(2分)
…(2分)函数y=f(x)的图象是一条抛物线,抛物线的顶点横坐标为
 ,
,开口向上,在(0,+∞) 上,当
 时函数取得最小值,
时函数取得最小值,所以
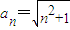 ;…(4分)
;…(4分) (2)将(1)中{an}的表达式代入,得
 .…(6分)
.…(6分)∴
 ,…(8分)
,…(8分) 所以所求的极限为:
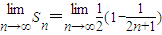 =
= ;…(10分)
;…(10分)(3)任取Ai、Aj(i、j∈N*,i≠j),设AiAj 所在直线的斜率为kij,
则
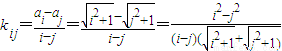 =
= .
.因此不存在满足条件的数对(i,j),使直线AiAj的斜率为1.…(16分)
点评:本题综合了数列与向量、数列与函数以及数列的极限等知识点,是一道难题.对思维的要求较高,考查了转化化归和函数与方程的数学思想.

练习册系列答案
相关题目
(理) 已知向量
=(2cosφ,2sinφ),φ∈(
,π),向量
=(0,-1),则向量
与
的夹角为( )
| a |
| π |
| 2 |
| b |
| a |
| b |
| A、φ | ||
B、
| ||
C、?-
| ||
D、
|
(理)已知向量
同时垂直于不共线向量
和
,若向量
=2
+
,则( )
| m |
| a |
| b |
| n |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上三种情况均有可能 |