Question

（04年北京卷文）(14分)

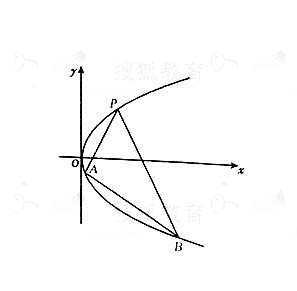
如图,抛物线关于x轴对称,它的顶点在坐标原点, 点P(1,2), A(x₁, y₁), B(x₂,y₂)均在直线上.

(Ⅰ)写出该抛物线的方程及其准线方程.

(Ⅱ)当PA与PB的斜率存在且倾角互补时,

求的值及直线AB的斜率.

Answer 1

解析:(Ⅰ)由已知条件,可设抛物线的方程为

∵点P(1,2)在抛物线上,

∴得=2.

  故所求抛物线的方程是

 准线方程是x=--1.

 (Ⅱ) 设直线PA的斜率为k_PA,直线PB的斜率为k_PB,

∵PA与PB的斜率存在且倾斜角互补,

∴

  由A(x₁,y₁), B(x₂,y₂)在抛物线上,得

   ①

        ②

  ∴

∴

∴

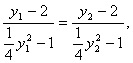
由①--②得直线AB的斜率

     (14分)