题目内容
设 、
、 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时,
 ,且
,且 ,则不等式
,则不等式

 0的解集是( )
0的解集是( )
A.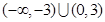 B.
B.
C. D.
D. 
【答案】
A
【解析】
试题分析:设F(x)=f (x)g(x),当x<0时,
∵F′(x)=f′(x)g(x)+f (x)g′(x)>0
∴F(x)在当x<0时为增函数
∵F(-x)=f (-x)g (-x)=-f (x)•g (x).?=-F(x).
故F(x)为(-∞,0)∪(0,+∞)上的奇函数.
∴F(x)在(0,∞)上亦为增函数
已知g(-3)=0,必有F(-3)=F(3)=0
构造如图的F(x)的图象,可知
F(x)<0的解集为x∈(-∞,-3)∪(0,3)
故选A
考点:本题主要考查了复合函数的求导运算和函数的单调性与其导函数正负之间的关系.导数是一个新内容,也是高考的热点问题,要多注意复习.
点评:解决该试题的关键是利用已知中导数的正负号,确定出函数F(x)=f (x)g(x)的单调性,以及奇偶性利用函数性质来得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 、
、 分别是定义在R上的奇函数和偶函数。当
分别是定义在R上的奇函数和偶函数。当 时,
时,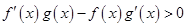 且
且 。则不等式
。则不等式 的解集是( )
的解集是( ) B.
B.
 D.
D.
 、
、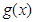 分别是定义在R上的奇函数和偶函数,当x<0时,
分别是定义在R上的奇函数和偶函数,当x<0时, >0且
>0且 ,则不等式
,则不等式 解集是( )
解集是( ) B.
B.
 D.
D.
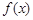 、
、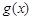 分别是定义在R上的奇函数和偶函数,当x<0时
分别是定义在R上的奇函数和偶函数,当x<0时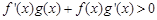 且
且 ,则不等式
,则不等式 的解集为
的解集为