题目内容
在直角标系xOy中,点(2,-2)在矩阵M=( )对应变换作用下得到点(-2,4),曲线C:x2+y2=1在矩阵M对应变换作用下得到曲线C',求曲线C'的方程.
)对应变换作用下得到点(-2,4),曲线C:x2+y2=1在矩阵M对应变换作用下得到曲线C',求曲线C'的方程.
【答案】分析:先根据变换的对应点,列式解出α=2,得M=( ).再设曲线C上任意一点P(x,y),根据矩阵变换的公式求出对应的点P′(x,y),解出由x、y表示x,y的式子,将点P的坐标代入曲线C方程,化简即得曲线C'的方程.
).再设曲线C上任意一点P(x,y),根据矩阵变换的公式求出对应的点P′(x,y),解出由x、y表示x,y的式子,将点P的坐标代入曲线C方程,化简即得曲线C'的方程.
解答:解:根据题意,得( )(
)( )=(
)=( )
)
∴2α=4,可得α=2,即M=( )
)
设P(x,y)是曲线C:x2+y2=1上任意一点,
则点P(x,y)在矩阵M对应的变换下变为点P′(x,y)
则有( )=(
)=( )(
)(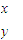 ),即
),即 ,所以
,所以
又∵点P在曲线C:x2+y2=1上,
∴ +x2=1,即曲线C'的方程为椭圆x2+
+x2=1,即曲线C'的方程为椭圆x2+ =1.
=1.
点评:本题给出矩阵变换,求曲线C在矩阵M对应变换作用下得到的曲线C'方程,着重考查了矩阵与变换的运算、曲线方程的求法等知识,属于中档题.利用求轨迹方程的方法进行求解,是解决本题的一般方法.
 ).再设曲线C上任意一点P(x,y),根据矩阵变换的公式求出对应的点P′(x,y),解出由x、y表示x,y的式子,将点P的坐标代入曲线C方程,化简即得曲线C'的方程.
).再设曲线C上任意一点P(x,y),根据矩阵变换的公式求出对应的点P′(x,y),解出由x、y表示x,y的式子,将点P的坐标代入曲线C方程,化简即得曲线C'的方程.解答:解:根据题意,得(
 )(
)( )=(
)=( )
)∴2α=4,可得α=2,即M=(
 )
)设P(x,y)是曲线C:x2+y2=1上任意一点,
则点P(x,y)在矩阵M对应的变换下变为点P′(x,y)
则有(
 )=(
)=( )(
)(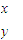 ),即
),即 ,所以
,所以
又∵点P在曲线C:x2+y2=1上,
∴
 +x2=1,即曲线C'的方程为椭圆x2+
+x2=1,即曲线C'的方程为椭圆x2+ =1.
=1.点评:本题给出矩阵变换,求曲线C在矩阵M对应变换作用下得到的曲线C'方程,着重考查了矩阵与变换的运算、曲线方程的求法等知识,属于中档题.利用求轨迹方程的方法进行求解,是解决本题的一般方法.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 分别是与x轴,y轴平行的单位向量,若直角三角形ABC中,
分别是与x轴,y轴平行的单位向量,若直角三角形ABC中, ,则实数m=( )。
,则实数m=( )。