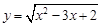题目内容
下列每组中两个函数是同一函数的组数共有( )
(1)f(x)=x2+1和f(v)=v2+1
(2)y=
和y=
(3)y=2x,x∈{0,1}和y=
x2+
x+1,x∈{0,1}
(4)y=1和y=x0
(5)y=
•
和y=
(6)y=x和y=
.
(1)f(x)=x2+1和f(v)=v2+1
(2)y=
| ||
| |x+2| |
| ||
| x+2 |
(3)y=2x,x∈{0,1}和y=
| 1 |
| 6 |
| 5 |
| 6 |
(4)y=1和y=x0
(5)y=
| x-1 |
| x-2 |
| x2-3x+2 |
(6)y=x和y=
| 3 | x3 |
| A、1组 | B、3组 | C、2组 | D、4组 |
分析:要判断两个函数是否是同一个函数,需要从三个方面来分析,即定义域,对应法则和值域,观察四个选项结果有三个的定义域不同,从而得出正确选项.
解答:解:(1)f(x)=x2+1和f(v)=v2+1,它们的定义域为R,对应法则相同,故是同一函数;
(2)y=
=
和y=
相同的定义域[-1,1],值域与对应法则,故它们是同一函数;
(3)y=2x,x∈{0,1}和y=
x2+
x+1,x∈{0,1}的定义域相同,对应法则不同,故不是同一函数;
(4)y=1和y=x0、y=1的定义域为R,y=x0的定义域为x≠0,两函数的定义域不同,故不是同一函数;
(5)y=
•
和y=
,不相同的定义域,故它们不是同一函数;
(6)y=x和y=
=x.相同的定义域R,值域与对应法则,故它们是同一函数;
是同一函数的组数共有3组,
故选B.
(2)y=
| ||
| |x+2| |
| ||
| x+2 |
| ||
| x+2 |
(3)y=2x,x∈{0,1}和y=
| 1 |
| 6 |
| 5 |
| 6 |
(4)y=1和y=x0、y=1的定义域为R,y=x0的定义域为x≠0,两函数的定义域不同,故不是同一函数;
(5)y=
| x-1 |
| x-2 |
| x2-3x+2 |
(6)y=x和y=
| 3 | x3 |
是同一函数的组数共有3组,
故选B.
点评:本题考查判断两个函数是否是同一函数,在开始学习函数的概念时,这是经常出现的一个问题,注意要从三个方面来分析:定义域、对应法则、值域,只有三要素完全相同,才能判断两个函数是同一个函数,这是判定两个函数为同一函数的标准.

练习册系列答案
相关题目
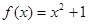 和
和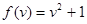 (2)
(2)
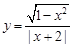 和
和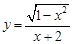
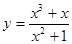 (4)
y=
(4)
y=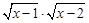 和
和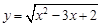
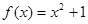 和
和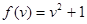 (2)
(2)
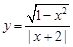 和
和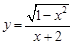
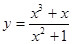 (4)
y=
(4)
y=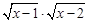 和
和