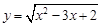题目内容
下列每组中两个函数是同一函数的组数共有( )
(1)f(x)=x2+1和f(v)=v2+1;(2)y=
和y=
;(3)y=1和y=x0;(4)y=
•
和y=
;(5)y=x和y=
.
(1)f(x)=x2+1和f(v)=v2+1;(2)y=
| ||
| |x+2| |
| ||
| x+2 |
| x-1 |
| x-2 |
| x2-3x+2 |
| 3 | x3 |
分析:分别判断两个函数的定义域和对应法则是否相同即可.
解答:解:(1)两个函数的定义域和对应法则相同,是相等函数.
(2)由1-x2≥0,解得-1≤x≤1,此时y=
=
,两个函数的定义域和对应法则相同,是相等函数.
(3)y=x0=1定义域为{x|x≠0},两个函数的定义域不相同,不是相等函数.
(4)由
得
,即x≥2,函数的定义域{x|x≥2},由x2-3x+2≥0,得x≥2或x≤1,即函数的定义域为{x|x≥2或x≤1},两个函数的定义域不相同,不是相等函数.
(5)y=
=x,两个函数的定义域和对应法则相同,是相等函数.
故选:C.
(2)由1-x2≥0,解得-1≤x≤1,此时y=
| ||
| |x+2| |
| ||
| x+2 |
(3)y=x0=1定义域为{x|x≠0},两个函数的定义域不相同,不是相等函数.
(4)由
|
|
(5)y=
| 3 | x3 |
故选:C.
点评:本题主要考查判断两个函数是否为同一函数,判断的依据主要是判断两个函数的定义域和对应法则是否相同.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
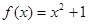 和
和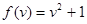 (2)
(2)
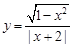 和
和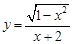
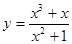 (4)
y=
(4)
y=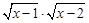 和
和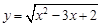
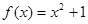 和
和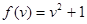 (2)
(2)
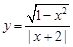 和
和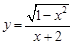
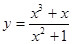 (4)
y=
(4)
y=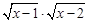 和
和