题目内容
观察图中各正方形图案,每条边上有n(n≥2)个圆点,第n个图案中圆点的个数是an,按此规律推断出所有圆点总和Sn与n的关系式为( )
A.Sn=2n2-2n
B.Sn=2n2
C.Sn=4n2-3n
D.Sn=2n2+2n
【答案】分析:先观察给出的正方形图案,将各圆点的个数列出来,探讨规律,将其转化为特殊的数列,再用求和公式求解.
解答:解:观察各个正方形图案可知各圆点的个数为:4,8,12,14,…
归纳为:圆点个数为首项为4,公差为4的等差数列,
因此所有圆点总和即为等差数列前n-1项和,
即Sn=(n-1)×4+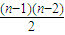 ×4=2n2-2n.
×4=2n2-2n.
故选A
点评:本题主要考查归纳推理,归纳其规律,体现了特殊到一般的思想方法,本题亦可用排除法,验证法等特殊法求解,如:当n=2时有S2=4,分别代入即可淘汰B,C,D三选项,从而选A.
解答:解:观察各个正方形图案可知各圆点的个数为:4,8,12,14,…
归纳为:圆点个数为首项为4,公差为4的等差数列,
因此所有圆点总和即为等差数列前n-1项和,
即Sn=(n-1)×4+
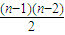 ×4=2n2-2n.
×4=2n2-2n.故选A
点评:本题主要考查归纳推理,归纳其规律,体现了特殊到一般的思想方法,本题亦可用排除法,验证法等特殊法求解,如:当n=2时有S2=4,分别代入即可淘汰B,C,D三选项,从而选A.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
观察图中各正方形图案,每条边上有n(n≥2)个圆点,第n个图案中圆点的个数是an,按此规律推断出所有圆点总和Sn与n的关系式为( )


| A、Sn=2n2-2n | B、Sn=2n2 | C、Sn=4n2-3n | D、Sn=2n2+2n |


