题目内容
观察如图中各正方形图案,每条边上有n(n≥2)个圆点,第n个图案中圆点的总数是Sn.按此规律推断出Sn与n的关系式为( )


分析:注意观察前三个图形中圆点的个数可以发现分别为:4,8,12,后一个图形中的圆点个数比前一个图形中圆点多4,所以可得Sn与n的关系式为:S=4n-4.
解答:解:n=2时,S2=4;n=3时,S3=4+1×4=8;n=4时,S4=4+2×4=12,
∴Sn=4+(n-2)×4=4n-4=4(n-1).
故选D.
∴Sn=4+(n-2)×4=4n-4=4(n-1).
故选D.
点评:此题属于规律性问题,解决此类问题,关键在观察、分析已知数据,寻找它们之间的以及与第一个图形的相互联系,探寻其规律.主要培养学生的观察能力和空间想象能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 个图案中圆点的总数是
个图案中圆点的总数是 .按此规律推断出
.按此规律推断出
 B.
B. D.
D.


 个图案中圆点的总数是
个图案中圆点的总数是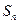 .按此规律推断出
.按此规律推断出


