题目内容
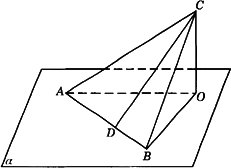
如下图,在△ABC中,∠ACB=90°,AB![]() 平面α,点
平面α,点![]() ,C在α内的射影为O,AC和BC与平面所成的角分别为30°和45°,CD是△ABC的AB边上的高线,求CD与平面α所成角的大小.
,C在α内的射影为O,AC和BC与平面所成的角分别为30°和45°,CD是△ABC的AB边上的高线,求CD与平面α所成角的大小.
答案:
解析:
解析:
|
解析:连结OD,∵CO⊥平面AOB,∴∠CDO为CD与平面α所成的角.∵AB、CB与平面α所成角分别为30°和45°,∴∠CAO=30°,∠CBO=45°.设CO=a,则AC=2a,OB=a, |

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 ,∵0°<∠CDO<90°,∴∠CDO=60°,即CD与平面α所成的角为60°.
,∵0°<∠CDO<90°,∴∠CDO=60°,即CD与平面α所成的角为60°.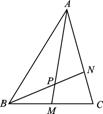
 =
= ,
,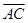 =
= ,AP的中点为Q,BQ的中点为R,CR的中点为P,若
,AP的中点为Q,BQ的中点为R,CR的中点为P,若 =m
=m ( )
( ) 




 =
= ,
, =
= ,AP的中点为Q,BQ的中点为R,CR的中点为P,若
,AP的中点为Q,BQ的中点为R,CR的中点为P,若 =m
=m ( )
( ) 
 B.
B. C.
C. D.
D.