题目内容
在数列1,1,2,3,5,8, ,21,34,55,…中,
,21,34,55,…中, 等于( )
等于( )
| A.11 | B.12 | C.13 | D.14 |
C
解析试题分析:观察所给数列的项,可知该数列从第三项起,后一项是前两项的和,设该数列为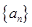 ,则该数列的递推关系式为:
,则该数列的递推关系式为: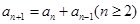 ,所以
,所以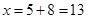 ,故选C.
,故选C.
考点:数列的概念.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}满足an = nkn(n∈N*,0 < k < 1),下面说法正确的是( )
①当 时,数列{an}为递减数列;
时,数列{an}为递减数列;
②当 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;
③当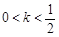 时,数列{an}为递减数列;
时,数列{an}为递减数列;
④当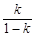 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项.
| A.①② | B.②④ | C.③④ | D.②③ |
数列 ,3,
,3, ,
, ,
, ,…,则9是这个数列的第( )
,…,则9是这个数列的第( )
| A.12项 | B.13项 | C.14项 | D.15项 |
数列 中的
中的 一个值等于
一个值等于
A. | B. | C. | D. |
[2013·江西抚州月考]数列{an}的前n项积为n2,那么当n≥2时,{an}的通项公式为( )
| A.an=2n-1 | B.an=n2 |
C.an= | D.an= |
若数列{an}满足 -
- =d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{
=d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{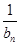 }为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( )
}为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( )
| A.10 | B.100 | C.200 | D.400 |
用正偶数按下表排列
| | 第1列 | 第2列 | 第3列 | 第4列 | 第5列 |
| 第一行 | | 2 | 4 | 6 | 8 |
| 第二行 | 16 | 14 | 12 | 10 | |
| 第三行 | | 18 | 20 | 22 | 24 |
| … | | … | 28 | 26 | |
A.第 251 行第 5 列
B.第 251 行第 1 列
C.第 250 行第 3 列
D.第 251 行第 5 列或第 252 行第 5列
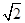 ,求证:a⊥b;
,求证:a⊥b; 中,角
中,角 的对边分别为
的对边分别为 向量
向量 ,
, ,且
,且 .
. 的值;
的值; ,
, ,求角
,求角 的大小及向量
的大小及向量 在
在 方向上的投影.
方向上的投影.