题目内容
关于下列命题:
①函数f(x)=loga(x-2)-1(a>0,a≠1)的图象恒过定点(3,-1);
②若函数y=f(x+1)的定义域是[-1,1],则y=f(x)的定义域是[-2,0];
③若函数y=f(x)是奇函数,当x<0时,f(x)=x2+5x,则f(2)=6
④设α∈{-1,
,
,1,2,3},则使幂函数y=xα为奇函数且在(0,+∞)上单调递增的α值的个数为3个
⑤若函数y=|2x-1|-m(m∈R)只有一个零点,则m≥1
其中正确的命题的序号是
①函数f(x)=loga(x-2)-1(a>0,a≠1)的图象恒过定点(3,-1);
②若函数y=f(x+1)的定义域是[-1,1],则y=f(x)的定义域是[-2,0];
③若函数y=f(x)是奇函数,当x<0时,f(x)=x2+5x,则f(2)=6
④设α∈{-1,
| 1 |
| 3 |
| 1 |
| 2 |
⑤若函数y=|2x-1|-m(m∈R)只有一个零点,则m≥1
其中正确的命题的序号是
①③⑤
①③⑤
( 注:把你认为正确的命题的序号都填上).分析:①函数f(x)=loga(x-2)-1(a>0,a≠1)的图象恒过定点(3,-1);②若函数y=f(x+1)的定义域是[-1,1],
则y=f(x)的定义域是[0,2];③若函数y=f(x)是奇函数,当x<0时,f(x)=x2+5x,则x>0时,f(x)=-x2+5x,由此能求出f(2);④设α∈{-1,
,
,1,2,3},则使幂函数y=xα为奇函数且在(0,+∞)上单调递增的α值的个数为2个;⑤由函数y=|2x-1|-m=
(m∈R)只有一个零点,能求出m的范围.
则y=f(x)的定义域是[0,2];③若函数y=f(x)是奇函数,当x<0时,f(x)=x2+5x,则x>0时,f(x)=-x2+5x,由此能求出f(2);④设α∈{-1,
| 1 |
| 3 |
| 1 |
| 2 |
|
解答:解:①函数f(x)=loga(x-2)-1(a>0,a≠1)的图象恒过定点(3,-1),故①正确;
②若函数y=f(x+1)的定义域是[-1,1],
则y=f(x)的定义域是[0,2],故②错误;
③若函数y=f(x)是奇函数,当x<0时,f(x)=x2+5x,
则x>0时,f(x)=-x2+5x,∴f(2)=-4+10=6,故③正确;
④设α∈{-1,
,
,1,2,3},
则使幂函数y=xα为奇函数且在(0,+∞)上单调递增的α值的个数为2个,
故④不正确;
⑤∵函数y=|2x-1|-m=
(m∈R)只有一个零点,
∴m≥1,故⑤正确.
故答案为:①③⑤.
②若函数y=f(x+1)的定义域是[-1,1],
则y=f(x)的定义域是[0,2],故②错误;
③若函数y=f(x)是奇函数,当x<0时,f(x)=x2+5x,
则x>0时,f(x)=-x2+5x,∴f(2)=-4+10=6,故③正确;
④设α∈{-1,
| 1 |
| 3 |
| 1 |
| 2 |
则使幂函数y=xα为奇函数且在(0,+∞)上单调递增的α值的个数为2个,
故④不正确;
⑤∵函数y=|2x-1|-m=
|
∴m≥1,故⑤正确.
故答案为:①③⑤.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在第一象限是增函数;
在第一象限是增函数;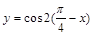 是奇函数;
是奇函数; 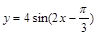 的一个对称中心是(
的一个对称中心是(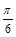 ,0);
,0);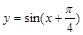 在闭区间
在闭区间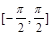 上是增函数.
上是增函数. 在第一象限是增函数;②函数
在第一象限是增函数;②函数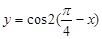 是偶函数;
是偶函数; 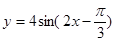 的一个对称中心是(
的一个对称中心是(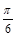 ,0);
,0); 在闭区间
在闭区间 上是增函数;
上是增函数;