题目内容
关于下列命题：
①函数y=tanx在第一象限是增函数；
②函数y=cos2(
-x)是偶函数；
③函数y=4sin(2x-
)的一个对称中心是（
，0）；
④cos（x+y）+cos（x-y）=2cosxcosy
⑤cos2α（1+tan2α）=1
写出所有正确的命题的题号：
①函数y=tanx在第一象限是增函数；
②函数y=cos2(
| π |
| 4 |
③函数y=4sin(2x-
| π |
| 3 |
| π |
| 6 |
④cos（x+y）+cos（x-y）=2cosxcosy
⑤cos2α（1+tan2α）=1
写出所有正确的命题的题号：
③④⑤
③④⑤
．分析：利用三角函数的性质对①取特值排除即可；
利用诱导公式可判断②；
③令f（x）=4sin（2x-
），可求得f（
）=0，从而可对③作出正确的判断；
④利用两角和与差的余弦计算即可判断其正误；
⑤将左端展开计算即可．
利用诱导公式可判断②；
③令f（x）=4sin（2x-
| π |
| 3 |
| π |
| 6 |
④利用两角和与差的余弦计算即可判断其正误；
⑤将左端展开计算即可．
解答：解：①∵x1=
，x2=
均为第一象限的角，且x1＜x2，但tanx1=1＞
=tanx2，故①函数y=tanx在第一象限是增函数，是错误的；
②∵y=f（x）=cos2（
-x）=sin2x，
∴f（-x）=sin（-2x）=-sin2x=-f（x），
∴y=cos2（
-x）为奇函数，故②错误；
③令f（x）=4sin（2x-
），则f（
）=4sin（2×
-
）=0，
∴函数y=4sin（2x-
）的一个对称中心是（
，0），即③正确；
④∵左端cos（x+y）+cos（x-y）=cosxcosy-sinxsiny+cosxcosy+sinxsiny=2cosxcosy=右端，
∴cos（x+y）+cos（x-y）=2cosxcosy，正确，即④正确；
⑤由于cos2α（1+tan2α）=cos2α+sin2α=1，故（5）正确．
综上所述，所有正确的命题的题号为③④⑤．
故答案为：③④⑤．
| π |
| 4 |
| 13π |
| 6 |
| ||
| 3 |
②∵y=f（x）=cos2（
| π |
| 4 |
∴f（-x）=sin（-2x）=-sin2x=-f（x），
∴y=cos2（
| π |
| 4 |
③令f（x）=4sin（2x-
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∴函数y=4sin（2x-
| π |
| 3 |
| π |
| 6 |
④∵左端cos（x+y）+cos（x-y）=cosxcosy-sinxsiny+cosxcosy+sinxsiny=2cosxcosy=右端，
∴cos（x+y）+cos（x-y）=2cosxcosy，正确，即④正确；
⑤由于cos2α（1+tan2α）=cos2α+sin2α=1，故（5）正确．
综上所述，所有正确的命题的题号为③④⑤．
故答案为：③④⑤．
点评：本题考查命题的真假判断与应用，着重考查三角函数的性质，考查两角和与差的余弦与基本关系式，属于中档题．
练习册系列答案
天天练口算系列答案
相关题目
在第一象限是增函数；
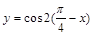是奇函数；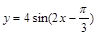 
的一个对称中心是（
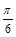，0）；
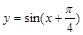在闭区间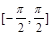
上是增函数.
在第一象限是增函数；②函数
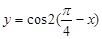是偶函数；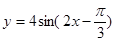 
的一个对称中心是（
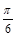，0）；
在闭区间
上是增函数;