题目内容
设x≥0,y≥0且x+2y=![]() ,求函数
,求函数![]() (8xy+4y2+1)的最大值与最小值.
(8xy+4y2+1)的最大值与最小值.
答案:
解析:
提示:
解析:
|
思想方法小结:一个一元二次函数同时有最大值和最小值,这只有在一闭区间上,才有可能.因此一定要注意P中的x(或y)的变化范围. |
提示:
|
考虑到对数函数的单调性,及底数小于1,问题归为求函数8xy+4y2+1的最小值与最大值.8xy+4y2+1是二元函数(即有二个自变量的函数),根据条件,将它化为一元函数(一般情况,多是化成一元二次函数),使问题进一步化归为求一元函数的最小值与最大值问题. |

练习册系列答案
相关题目

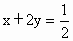 ,求函数
,求函数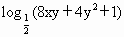 的最大值与最小值.
的最大值与最小值.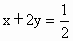 ,求函数
,求函数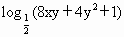 的最大值与最小值.
的最大值与最小值.