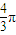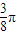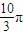题目内容
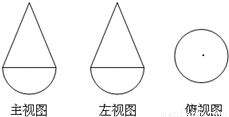
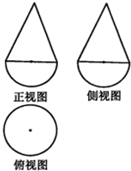己知一个几何体是由上、下两部分构成的组合体，其三视图如图，若图中圆的半径为1，等腰三角形的腰长为| 5 |
分析：三视图可知几何体是下部为半球，上部是圆锥，根据三视图的数据特征，求出几何体的体积．
解答：解：由题意组合体的上部是圆锥，底面半径为：1；母线为：
，所以圆锥的高为：2；
下部是半球，底面半径为：1，所以组合体的体积为：
13+
×12π×2=
．
故答案为：
| 5 |
下部是半球，底面半径为：1，所以组合体的体积为：
| 2π |
| 3 |
| 1 |
| 3 |
| 4π |
| 3 |
故答案为：
| 4π |
| 3 |
点评：本题是基础题，考查组合体的三视图的复原特征的判断，考查空间想象能力，计算能力．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
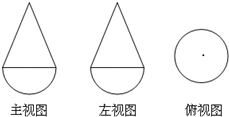己知一个几何体是由上、下两部分构成的组合体，其三视图如下图，若图中圆的半径为1，等腰三角形的腰长为| 5 |
A、
| ||
| B、2π | ||
C、
| ||
D、
|
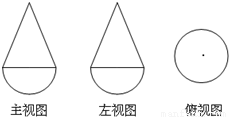
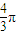
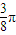
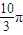
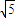，则该几何体的体积是（ ）
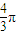
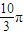
，则该几何体的体积是（ ）
，则该几何体的体积是（ ）
