题目内容
16.已知两直线l1:x-2y+4=0和l2:x+y-2=0的交点为P.(1)直线l过点P且与直线5x+3y-6=0垂直,求直线l的方程;
(2)圆C过点(3,1)且与l1相切于点P,求圆C的方程.
分析 (1)联立方程组,求出直线l1:x-2y+4=0和l2:x+y-2=0的交点,再求出直线l的斜率,可得直线l的方程;
(2)设圆方程为标准方程,求出圆心与半径,即可求得圆的方程.
解答 解:(1)联立方程组$\left\{\begin{array}{l}{x-2y+4=0}\\{x+y-2=0}\end{array}\right.$,解得x=0,y=2,
∴直线l1:x-2y+4=0和l2:x+y-2=0的交点P(0,2),
又∵直线5x+3y-6=0的斜率为-$\frac{5}{3}$,∴直线l的斜率为$\frac{3}{5}$,
∴直线l的方程为y-2=$\frac{3}{5}$(x-0),化为一般式可得3x-5y+10=0.
(2)设圆方程为标准方程(x-a)2+(y-b)2=r2,
∴a2+(b-2)2=(a-3)2+(b-1)2=$\frac{|a-2b+4|}{\sqrt{5}}$=r2,
∴a=1,b=0,
∴圆的方程为(x-1)2+y2=5.
点评 本题考查直线、圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
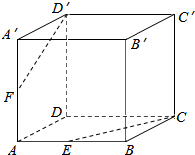
6.如图,正方体ABCD-A′B′C′D′中,AB的中点为E,AA′的中点为F,则直线D′F和直线CE( )

| A. | 都与直线DA相交,且交于同一点 | B. | 互相平行 | ||
| C. | 异面 | D. | 都与直线DA相交,但交于不同点 |
4.函数f(x)=ex+2x-4的零点所在的区间是( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | (1,$\frac{3}{2}$) |
11.有一组实验数据如下:
现在用下列函数中的一个近似地表示这些数据满足的规律,其中最恰当的一个是( )
| x | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| y | 1.5 | 4.04 | 7.5 | 12.5 | 18.27 |
| A. | y=log2x | B. | $y={log_{\frac{1}{2}}}x$ | C. | $y=\frac{{{x^2}-1}}{2}$ | D. | $y=2x-\frac{1}{2}$ |
 已知函数f(x)=x|x-1|.
已知函数f(x)=x|x-1|.