题目内容
已知直线y=kx+1与双曲线3x2-y2=1有A、B两个不同的交点，（1）如果以AB为直径的圆恰好过原点，试求k的值；（2）是否存在k的值，使得两个不同的交点A、B关于直线y=2x对称.
思路解析：（1）要求k的值，必须建立关于k的方程，由已知OA⊥OB，所以kOA·kOB=-1，及A、B既在直线上，又在双曲线上可得k的值.（2）为开放性题目，一般方法为：假设存在，根据已知求解，若解出而且符合题意则存在，若无解或解出不符合题意，则不存在. 解：（1）设A（x1,kx1+1）,B(x2,kx2+1)，则以AB为直径的圆过原点的充要条件是（ 即(k2+1)x1x2+k(x1+x2)+1=0. ① 由方程组 ∴x1+x2= 解得k2=1,∴k=1或k=-1,当k=1时，方程②为2x2-2x-2=0,有两个不等实根；当k=-1时，方程②为x2+x-1=0,有两个不等实根,故k=±1时，以AB为直径的圆过原点. （2）若A（x1，kx1+1）,B(x2,kx2+1)关于y=2x对称， 则 ④整理得(k-2)(x1+x2)+2=0. ∵x1+x2= 这个结果与③矛盾，故不存在k的值，使A、B两点关于直线y=2x对称.
）·（
）=-1,
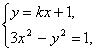消去y,得（3-k2）x2-2kx-2=0. ②
,x1x2=
，代入①得
+
+1=0,
,∴
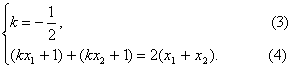
+2=0,解得k=
.
新目标英语阅读训练系列答案
名师学案英语高考新题型系列答案
新课程课堂同步练习册系列答案
鼎尖训练系列答案
初中生学业评价指导用书系列答案
阅读计划初中课外现代文拓展阅读系列答案
伴你学习新课程单元过关练习系列答案
中考综合学习评价与检测系列答案
新课程初中学习能力自测丛书系列答案
初中毕业升学考试指导系列答案
| x2 |
| 2 |
| y2 |
| m |
| A、（1，2] |
| B、[1，2） |
| C、[1，2）∪[2，+∞） |
| D、（2，+∞） |