题目内容
某班在联欢会上举行一个抽奖活动,甲箱中有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
(Ⅰ)0.2(Ⅱ)

本试题主要是考查了相互独立事件的概率的乘法公式以及n次独立重复试验中事件发生的概率的综合运用。
(1)因为甲箱中有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
则求每个活动参加者获奖的概率利用独立事件概率的乘法公式直接求解。
(2)根据办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖,有三种情况分类讨论得到结论。
解:(Ⅰ)设事件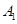 表示从甲箱中摸出红球,事件
表示从甲箱中摸出红球,事件 表示从乙箱中摸出红球.
表示从乙箱中摸出红球.
因为从甲箱中摸球的结果不影响从乙箱中摸球的结果,所以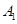 和
和 相互独立.
相互独立.

所以 .————7分
.————7分
(Ⅱ)设 为5人中获奖的人次,则
为5人中获奖的人次,则 , —————————9分
, —————————9分


 .
.
所以,5人中至少有3人获奖的概率为 . ————————13分
. ————————13分
(1)因为甲箱中有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
则求每个活动参加者获奖的概率利用独立事件概率的乘法公式直接求解。
(2)根据办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖,有三种情况分类讨论得到结论。
解:(Ⅰ)设事件
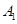 表示从甲箱中摸出红球,事件
表示从甲箱中摸出红球,事件 表示从乙箱中摸出红球.
表示从乙箱中摸出红球.因为从甲箱中摸球的结果不影响从乙箱中摸球的结果,所以
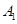 和
和 相互独立.
相互独立.
所以
 .————7分
.————7分(Ⅱ)设
 为5人中获奖的人次,则
为5人中获奖的人次,则 , —————————9分
, —————————9分

 .
.所以,5人中至少有3人获奖的概率为
 . ————————13分
. ————————13分
练习册系列答案
相关题目
 ,取到方片的概率是
,取到方片的概率是 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:


















 ,
, ,
, 的3个黑球和编号为
的3个黑球和编号为 ,
, 的2个红球,从中任意摸出2个球.
的2个红球,从中任意摸出2个球.  和
和 ,求关于x的方程
,求关于x的方程 有实数根的概率
有实数根的概率 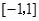 任取两个实数
任取两个实数 ,则关于
,则关于 的二次方程
的二次方程 有两个不相等的实数根的概率是 .
有两个不相等的实数根的概率是 .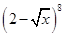 展开式中不含
展开式中不含 项的系数的和为( )
项的系数的和为( ) ,则
,则 的值为( )
的值为( ) 


