��Ŀ����
����P��1��0��������C��y=xk��x�ʣ�0��+�ޣ���k��N*��k��1�������ߣ��е�ΪM1����M1��x���ϵ�ͶӰ�ǵ�P1���ֹ���P1������C�����ߣ��е�ΪM2����M2��x���ϵ�ͶӰ�ǵ�P2������������ȥ���õ�һϵ�е�M1��M2����Mn�����������ǵĺ�����a1��a2������
an����������Ϊ{an}��
����������{an}��ͨ�ʽ��
������֤��an��1+
��
����k=2ʱ����bn=
��������{bn}��ǰn���Sn��
an����������Ϊ{an}��
����������{an}��ͨ�ʽ��
������֤��an��1+
| n |
| k-1 |
����k=2ʱ����bn=
| n |
| an |
����y=xk������
��y��=kxk-1��
����Mn��an��ank�������߷�����y-ank=kank-1��x-an��������2�֣�
��n=1ʱ�����߹���P��1��0����
��0-a1k=ka1k-1��1-a1����
��a1=
��
��n��1ʱ�����߹���Pn-1��an-1��0����
��0-ank=kank-1��an-1-an����
��
=
��
��������{an}������a1=
������Ϊ
�ĵȱ����У�
��������{an}��ͨ�ʽΪan=(
)n��n��N*������4�֣�
�� II��Ӧ�ö���ʽ��������an=(
)n=(1+
)n=
+
+
(
)2+��+
(
)n��1+
������8�֣�
�� III����k=2ʱ��an=2n��
����{bn}��ǰn���Sn=
+
+
+��+
��
ͬ����
����
Sn=
+
+
+��+
��
��ʽ���������10�֣�
��
Sn=
+
+
+��+
-
=
-
=1-
-
��
����Sn=2-
������12�֣�
��y��=kxk-1��
����Mn��an��ank�������߷�����y-ank=kank-1��x-an��������2�֣�
��n=1ʱ�����߹���P��1��0����
��0-a1k=ka1k-1��1-a1����
��a1=
| k |
| k-1 |
��n��1ʱ�����߹���Pn-1��an-1��0����
��0-ank=kank-1��an-1-an����
��
| an |
| an-1 |
| k |
| k-1 |
��������{an}������a1=
| k |
| k-1 |
| k |
| k-1 |
��������{an}��ͨ�ʽΪan=(
| k |
| k-1 |
�� II��Ӧ�ö���ʽ��������an=(
| k |
| k-1 |
| 1 |
| k-1 |
| C | 0n |
| C | 1n |
| 1 |
| k-1 |
| C | 2n |
| 1 |
| k-1 |
| C | nn |
| 1 |
| k-1 |
| n |
| k-1 |
�� III����k=2ʱ��an=2n��
����{bn}��ǰn���Sn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
ͬ����
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
��ʽ���������10�֣�
��
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n+1 |
| 1 |
| 2n |
| n |
| 2n+1 |
����Sn=2-
| n+2 |
| 2n |

��ϰ��ϵ�д�
 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д�
�����Ŀ

 ��2009•����һģ������P��1��0��������C��y=x2��x��0�������ߣ��е�ΪQ1��ûQ1��x���ϵ�ͶӰ��P1���ֹ�P1��������C�����ߣ��е�ΪQ2����Q2��x���ϵ�ͶӰ��P2����������ȥ���õ�һϵ�е�Q1Q2����Qn����Qn�ĺ�����Ϊan��
��2009•����һģ������P��1��0��������C��y=x2��x��0�������ߣ��е�ΪQ1��ûQ1��x���ϵ�ͶӰ��P1���ֹ�P1��������C�����ߣ��е�ΪQ2����Q2��x���ϵ�ͶӰ��P2����������ȥ���õ�һϵ�е�Q1Q2����Qn����Qn�ĺ�����Ϊan��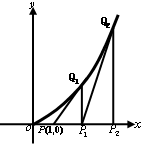 ��2013•�عض�ģ����ͼ������P��1��0��������C��y=x2��x�ʣ�0��+�ޣ��������ߣ��е�ΪQ1�����Q1��x���ϵ�ͶӰ�ǵ�P1���ֹ���P1������C�����ߣ��е�ΪQ2����Q2��x���ϵ�ͶӰ��P2������������ȥ���õ�һϵ�е�Q1��Q2��Q3-Qn�����Qn�ĺ�����Ϊan��
��2013•�عض�ģ����ͼ������P��1��0��������C��y=x2��x�ʣ�0��+�ޣ��������ߣ��е�ΪQ1�����Q1��x���ϵ�ͶӰ�ǵ�P1���ֹ���P1������C�����ߣ��е�ΪQ2����Q2��x���ϵ�ͶӰ��P2������������ȥ���õ�һϵ�е�Q1��Q2��Q3-Qn�����Qn�ĺ�����Ϊan��