题目内容
如图，椭圆C的中心在原点，焦点在x轴上，F1，F2分别是椭圆C的左、右焦点，M是椭圆短轴的一个端点，过F1的直线l与椭圆交于A，B两点，△MF1F2的面积为4，△ABF2的周长为
（Ⅰ）求椭圆C的方程；
（Ⅱ）设点Q的坐标为（1，0），是否存在椭圆上的点P及以Q为圆心的一个圆，使得该圆与直线PF1，PF2都相切，如存在，求出P点坐标及圆的方程，如不存在，请说明理由．
【答案】分析：（I）根据三角形的面积公式及椭圆的定义列出关于椭圆的三个参数a，b，c的关系，再加上a，b，c本身的关系，通过解方程求出a，b，c，写出椭圆的方程．
（II）假设存在满足条件的点p，设出其坐标，根据两点式写出直线PF1，PF2的方程，根据圆的切线满足圆心到直线的距离等于半径，利用点到直线的距离公式列出有关点p的坐标的方程，再利用点p的坐标满足椭圆的方程，解方程组求得点p的坐标．
解答：解：（Ⅰ） 由题意知：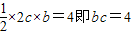
又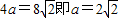
，
∵a2=b2+c2
解得 b=c=2
∴椭圆的方程为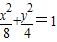
（Ⅱ）假设存在椭圆上的一点P（x，y），使得直线PF1，PF2与以Q为圆心的圆相切，
则Q到直线PF1，PF2的距离相等，
∵F1（-2，0），F2（2，0）
∴PF2：（x-2）y-yx+2y=0； PF1：（x+2）y-yx-2y=0
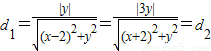
化简整理得：8x2-40x+32+8y2=0
∵点在椭圆上，
∴x2+2y2=8
解得：x=2或 x=8（舍）
x=2时，
，r=1，
∴椭圆上存在点P，其坐标为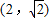
或
，
使得直线PF1，PF2与以Q为圆心的圆（x-1）2+y2=1相切
点评：求圆锥曲线的方程一般利用待定系数法，要注意椭圆的三个参数的关系为：a2=b2+c2；解决是否存在性问题，一般先假设存在，然后利用已知条件求，若求出即存在，求不出，说明不存在．
（II）假设存在满足条件的点p，设出其坐标，根据两点式写出直线PF1，PF2的方程，根据圆的切线满足圆心到直线的距离等于半径，利用点到直线的距离公式列出有关点p的坐标的方程，再利用点p的坐标满足椭圆的方程，解方程组求得点p的坐标．
解答：解：（Ⅰ） 由题意知：
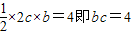
又
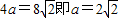，∵a2=b2+c2
解得 b=c=2
∴椭圆的方程为
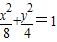
（Ⅱ）假设存在椭圆上的一点P（x，y），使得直线PF1，PF2与以Q为圆心的圆相切，
则Q到直线PF1，PF2的距离相等，
∵F1（-2，0），F2（2，0）
∴PF2：（x-2）y-yx+2y=0； PF1：（x+2）y-yx-2y=0
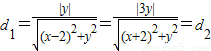
化简整理得：8x2-40x+32+8y2=0
∵点在椭圆上，
∴x2+2y2=8
解得：x=2或 x=8（舍）
x=2时，
，r=1，∴椭圆上存在点P，其坐标为
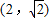或，使得直线PF1，PF2与以Q为圆心的圆（x-1）2+y2=1相切
点评：求圆锥曲线的方程一般利用待定系数法，要注意椭圆的三个参数的关系为：a2=b2+c2；解决是否存在性问题，一般先假设存在，然后利用已知条件求，若求出即存在，求不出，说明不存在．
练习册系列答案
相关题目
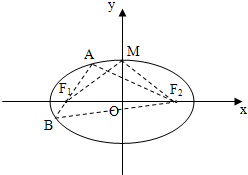如图，椭圆C的中心在原点，焦点在x轴上，F1，F2分别是椭圆C的左、右焦点，M是椭圆短轴的一个端点，过F1的直线l与椭圆交于A，B两点，△MF1F2的面积为4，△ABF2的周长为
已知椭圆C的中心在坐标原点，焦点在x轴上，左、右焦点分别为F1，F2，且|F1F2|=2，点P（1，
如图，在平面直角坐标系xOy中，椭圆C的中心在坐标原点O，右焦点为F．若C的右准线l的方程为x=4，离心率e=
如图，椭圆C的中心在原点，焦点在x轴上，F1，F2分别是椭圆C的左、右焦点，M是椭圆短轴的一个端点，过F1的直线l与椭圆交于A，B两点，△MF1F2的面积为4，△ABF2的周长为