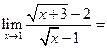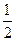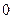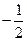Question

设等差数列{a_n}满足3a₈=5a₁₃，且a₁＞0，S_n是前n项和，则前______项和最大？

Answer 1

设等差数列{a_n}的公差为d，
则3（a₁+7d）=5（a₁+12d），
解得d=-

2

39

a1＜0，
故a_n=a₁+（n-1）d=

41-2n

39

a1，
令

41-2n

39

a1≤0，结合a₁＞0可得n≥

41

2

，
故等差数列{a_n}的前20项为正，从第21项开始为负值，
故数列的前20项和最大，
故答案为：20