题目内容
给出下列命题:
①当a≥1时,不等式|x-4|+|x-3|<a的解集非空
②存在一圆与直线系xcosθ+ysinθ=1(x∈R)都相切
③已知(x+2)2+
=1,则x2+y2的取值范围是[1,
]
④底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
⑤函数y=f(x+2)和y=f(2-x)的图象关于直线x=2对称.
其中正确的有
①当a≥1时,不等式|x-4|+|x-3|<a的解集非空
②存在一圆与直线系xcosθ+ysinθ=1(x∈R)都相切
③已知(x+2)2+
| y2 |
| 4 |
| 28 |
| 3 |
④底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
⑤函数y=f(x+2)和y=f(2-x)的图象关于直线x=2对称.
其中正确的有
②③⑤
②③⑤
.分析:①根据绝对值的几何意义来判断,当a=1时,为空集;
②找出一个圆,x2+y2=1,满足条件.
③用参数法,设x=-2+cosα,y=2sinα,用cosα表示出x2+y2,转化成一元二次函数求最值.
④根据正三棱锥的定义,每个面都是正三角形的三棱锥是正三角形.
⑤函数y=f(x+2)和y=f(2-x)的图象关于直线x=2对称.
②找出一个圆,x2+y2=1,满足条件.
③用参数法,设x=-2+cosα,y=2sinα,用cosα表示出x2+y2,转化成一元二次函数求最值.
④根据正三棱锥的定义,每个面都是正三角形的三棱锥是正三角形.
⑤函数y=f(x+2)和y=f(2-x)的图象关于直线x=2对称.
解答:解:①|x-4|+|x-3|的几何意义是到3的距离与到4的距离和,最小值为为1,若a=1时,不等式|x-4|+|x-3|<1的解集为空,①错误;
②x2+y2=1与直线系xcosθ+ysinθ=1都相切,②正确;
③设x=-2+cosα,y=2sinα.则x2+y2=4+cos2α-4cosα+4sin2α=-3cos2α-4cosα+8(cosα∈(-1,1)),当cosα=1时,取最大值最小值,为1;当cos=-
时,取最大值.为
,.正确.
④正三棱锥的每个面都是正三角形,④错误;
⑤函数y=f(x+2)和y=f(2-x)的图象关于直线x=2对称.正确
故答案为:②③⑤.
②x2+y2=1与直线系xcosθ+ysinθ=1都相切,②正确;
③设x=-2+cosα,y=2sinα.则x2+y2=4+cos2α-4cosα+4sin2α=-3cos2α-4cosα+8(cosα∈(-1,1)),当cosα=1时,取最大值最小值,为1;当cos=-
| 2 |
| 3 |
| 28 |
| 3 |
④正三棱锥的每个面都是正三角形,④错误;
⑤函数y=f(x+2)和y=f(2-x)的图象关于直线x=2对称.正确
故答案为:②③⑤.
点评:本题考查了绝对值的几何意义,参数法等基本知识,综合性比较强,应灵活掌握.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
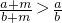 ,则a<b;
,则a<b;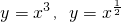 的图象都在直线y=x的上方;;
的图象都在直线y=x的上方;;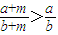 ,则a<b;
,则a<b;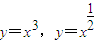 的图象都在直线y=x的上方;;
的图象都在直线y=x的上方;;