题目内容
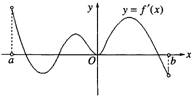
函数f(x)在(a，b)上连续，且
f(x)=m，
f(x)=n，mn＜0，f′(x)＞0，则f（x）=0在（a，b）内（ ）
| lim |
| x→a+ |
| lim |
| x→b- |
分析：由题意可得函数f（x）在在（a，b）上单调递增，f（a）f（b）＜0，故函数（x）在在（a，b）上有唯一零点，由此得出
结论．
结论．
解答：解：由题意可得函数f（x）在在（a，b）上单调递增，f（a）=m，f（b）=n，
∵mn＜0，∴f（a）f（b）＜0．
故函数（x）在在（a，b）上有唯一零点，即 方程f（x）=0 在（a，b）上有且只有一个实数根，
故选D．
∵mn＜0，∴f（a）f（b）＜0．
故函数（x）在在（a，b）上有唯一零点，即 方程f（x）=0 在（a，b）上有且只有一个实数根，
故选D．
点评：本题主要考查极限及其运算法则的应用，函数在某点连续的意义，属于基础题．
练习册系列答案
相关题目
]上的面积为
（n∈N＊），（ⅰ）y＝sin3x在[0,
]上的面积为 ；（ⅱ）y＝sin（3x－π）＋1在[
，
]上的面积为 。