题目内容
10.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知sinA+sinC=psinB(p>0),且ac=$\frac{1}{4}$b2,若∠B为锐角,求p的取值范围是( )| A. | $\frac{\sqrt{6}}{2}$<p<$\sqrt{2}$ | B. | 1<p<$\sqrt{2}$ | C. | 1<p<$\frac{\sqrt{6}}{2}$ | D. | 1<p<$\frac{\sqrt{6}}{2}$或$\frac{\sqrt{6}}{2}$<p<$\sqrt{2}$ |
分析 已知第一个等式利用正弦定理化简,再利用基本不等式变形,将第二个等式代入求出p的范围,再由B为锐角,得出cosB的范围,利用余弦定理表示出cosB,整理变形后求出p的范围,综上,得出满足题意p的范围即可.
解答 解:已知等式sinA+sinC=psinB(p>0),利用正弦定理化简得:a+c=pb>2$\sqrt{ac}$,
把ac=$\frac{1}{4}$b2代入得:a+c=pb>b,即p>1,
∵B为锐角,
∴0<cosB<1,即0<$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}}{2ac}$-2<1,
∵$\frac{{a}^{2}+{c}^{2}}{2ac}$-2=$\frac{(a+c)^{2}}{2ac}$-3=2p2-3,
∴0<2p2-3<1,
解得:$\frac{\sqrt{6}}{2}$<p<$\sqrt{2}$,
综上,p的取值范围为$\frac{\sqrt{6}}{2}$<p<$\sqrt{2}$,
故选:A.
点评 此题考查了正弦、余弦定理,基本不等式的运用,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
18.已知f(x)=ex(sinx-cosx)(0≤x≤2015π),则函数f(x)的各极大值之和为( )
| A. | $\frac{{{e^x}({1-{e^{2014π}}})}}{{1-{e^{2π}}}}$ | B. | 10082π | ||
| C. | $\frac{{{e^{2x}}({1-{e^{2014π}}})}}{{1-{e^{2π}}}}$ | D. | 1008π |
19.已知函数f(x)是定义在R上的奇函数,且f(x-1)为偶函数,当x∈[0,1]时,f(x)=${x}^{\frac{1}{2}}$,若函数g(x)=f(x)-x-b有三个零点,则实数b的取值集合是(以下k∈Z)( )
| A. | (2k-$\frac{1}{4}$,2k+$\frac{1}{4}$) | B. | (2k+$\frac{1}{2}$,2k+$\frac{5}{2}$) | C. | (4k-$\frac{1}{4}$,4k+$\frac{1}{4}$) | D. | (4k+$\frac{1}{2}$,4k+$\frac{9}{2}$) |
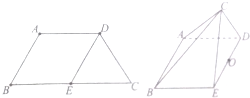 如图,ABCD为等腰梯形,且AD∥BC,E为BC的中点,AB=AD=BE,沿DE将△CDE折起成四棱锥C-ABED.
如图,ABCD为等腰梯形,且AD∥BC,E为BC的中点,AB=AD=BE,沿DE将△CDE折起成四棱锥C-ABED.