题目内容
若直线y=x+t与椭圆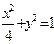 相交于A、B两点,当t变化时,求|AB|的最大值.
相交于A、B两点,当t变化时,求|AB|的最大值.
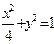 相交于A、B两点,当t变化时,求|AB|的最大值.
相交于A、B两点,当t变化时,求|AB|的最大值.|AB|取最大值为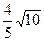 .
.
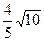 .
.以y= x +t代入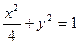 ,并整理得
,并整理得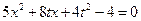 ①
①
因为直线与椭圆相交,则△=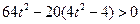 ,
,
所以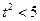 ,即
,即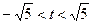 ,
,
设A(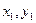 ),B(
),B(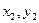 ),则A(
),则A(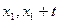 ),B(
),B(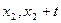 ),
),
且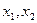 是方程①的两根.
是方程①的两根.
由韦达定理可得: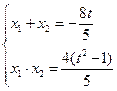 , 所以,
, 所以,
弦长|AB|2=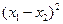 +
+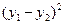
=2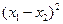 =2[
=2[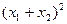
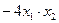 ]
]
=2[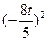
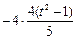 ]
]
得 |AB|=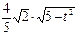
所以当t=0时,|AB|取最大值为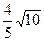 .
.
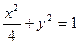 ,并整理得
,并整理得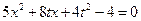 ①
①因为直线与椭圆相交,则△=
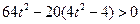 ,
,所以
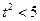 ,即
,即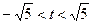 ,
,设A(
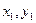 ),B(
),B(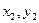 ),则A(
),则A(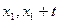 ),B(
),B(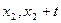 ),
),且
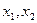 是方程①的两根.
是方程①的两根.由韦达定理可得:
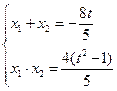 , 所以,
, 所以,弦长|AB|2=
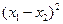 +
+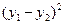
=2
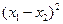 =2[
=2[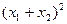
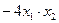 ]
]=2[
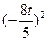
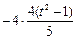 ]
]得 |AB|=
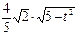
所以当t=0时,|AB|取最大值为
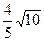 .
.
练习册系列答案
相关题目
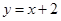 与函数
与函数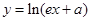 的图象相切,其中
的图象相切,其中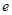 是自然对数的底,则
是自然对数的底,则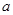 为( )
为( )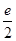







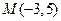 ,
,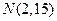 .在直线
.在直线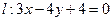 上的找一点
上的找一点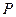 ,使
,使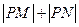 最小,并求出最小值.
最小,并求出最小值.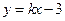 与线段AB相交,求
与线段AB相交,求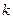 的取值范围.
的取值范围. 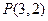 与点
与点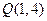 关于直线
关于直线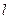 对称,则直线
对称,则直线



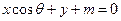 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )


