题目内容
已知M是面积为1的△ABC内的一点,若△MBC,△MCA,△MAB的面积分别为
,x,y,则
+
的最小值为( )
| 1 |
| 2 |
| 1 |
| x |
| 4 |
| y |
分析:由题意写出x、y所满足的关系式,然后用“1的代换”化简,再用均值不等式求最值
解答:解:由题意知x>0,y>0,且x+y=
∴2x+2y=1
∴
+
=(
+
)×1=(
+
) ×(2x+2y)=10+
+
又x>0,y>0
∴
>0,
>0
∴
+
=10+
+
≥10+2
10+8=18
当
,即当
(舍) 或
时等号成立,取得最小值18
故选B
| 1 |
| 2 |
∴2x+2y=1
∴
| 1 |
| x |
| 4 |
| y |
| 1 |
| x |
| 4 |
| y |
| 1 |
| x |
| 4 |
| y |
| 2y |
| x |
| 8x |
| y |
又x>0,y>0
∴
| 2y |
| x |
| 8x |
| y |
∴
| 1 |
| x |
| 4 |
| y |
| 2y |
| x |
| 8x |
| y |
|
当
|
|
|
故选B
点评:本题考查均值不等式,要注意均值不等式的条件.属简单题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB. ,x,y,则
,x,y,则 的最小值为
的最小值为 ,x,y,则
,x,y,则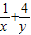 的最小值为( )
的最小值为( )