题目内容
已知椭圆C: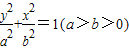 的离心率为
的离心率为 ,上、下顶点分别为A1,A2,椭圆上的点到上焦点F1的距离的最小值为1.
,上、下顶点分别为A1,A2,椭圆上的点到上焦点F1的距离的最小值为1.(1)求椭圆C的标准方程.
(2)以原点为顶点,F1为焦点的抛物线上的点P(非原点)处的切线与x轴,y轴分别交于Q、R两点,若
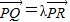 ,求λ的值.
,求λ的值.(3)是否存在过点(0,m)的直线l,使得l与椭圆相交于A、B两点(A、B不是上、下顶点)且满足
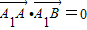 ,若存在,求出实数m的值;若不存在,请说明理由.
,若存在,求出实数m的值;若不存在,请说明理由.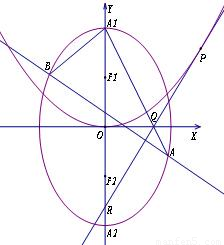
【答案】分析:(1)椭圆上的点在上顶点时到上焦点F1的距离的最小,进而根据椭圆的离心率求得a和c,进而根据b2=a2-c2,求得b,椭圆的方程可得.
(2)先求得椭圆的焦点坐标,进而可得抛物线方程,进而对抛物线方程进行求导,设出p点坐标,则可知该点出的切线的斜率,则切线方程可得.进而求出Q和R的坐标,进而表示出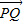 和
和 进而求得λ.
进而求得λ.
(3)假设存在过点(0,m)的直线l,满足条件,则l的斜率必存在,进而可设直线方程与椭圆联立方程消去y,设A(x1,y1),B(x2,y2)根据判别式大于0求得m的范围,根据韦达定理可表示出x1+x2和x1x2,进而表示出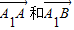 根据
根据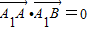 求得m的值,最后进行检验看m是否符合.
求得m的值,最后进行检验看m是否符合.
解答:解:(1)依题意得: ,∴
,∴ ,∴b2=a2-c2=3
,∴b2=a2-c2=3
∴所求的椭圆方程为: .
.
(2)由(1)知,F1(0,1)则抛物线的方程为x2=4y
即
设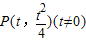 则该点处的切线的斜率
则该点处的切线的斜率
∴切线方程为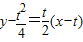
令 令
令
∴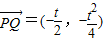

∴ 即
即 .
.
(3)假设存在过点(0,m)的直线l,满足条件,则l的斜率必存在,
∴可设l方程为y=kx+m联立 消去y得(4+3k2)x2+6mkx+3(m2-4)=0,
消去y得(4+3k2)x2+6mkx+3(m2-4)=0,
设A(x1,y1),B(x2,y2)
则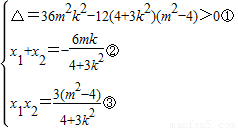
由①得4+3k2-m2>0
由②③及直线l的方程得y1y2=(kx1+m)(kx2+m)=k2x1x2+mk(x1+x2)+m2
=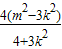 y1+y2=(kx1+m)+(kx2+m)=k(x1+x2)+2m
y1+y2=(kx1+m)+(kx2+m)=k(x1+x2)+2m
=
∵椭圆的上顶点为A1(0,2),
∴x1x2+(y1-2)(y2-2)=0即x1x2+y1y2-2(y1+y2)+4=0
∴
整理得7m2-16m+4=0解得
当m=2时,直线l的方程为y=kx+2过椭圆的上顶点A1(0,2)与已知矛盾
当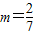 时,直线l的方程为
时,直线l的方程为 符合题意
符合题意
∴存在过点(0,m)的直线l,使得l与椭圆相交于A、B两点,且满足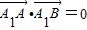 ,实数m的值为
,实数m的值为
点评:本题主要考查了椭圆的标准方程和直线与椭圆的关系.考查了学生对圆锥曲线知识的综合掌握.
(2)先求得椭圆的焦点坐标,进而可得抛物线方程,进而对抛物线方程进行求导,设出p点坐标,则可知该点出的切线的斜率,则切线方程可得.进而求出Q和R的坐标,进而表示出
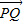 和
和 进而求得λ.
进而求得λ.(3)假设存在过点(0,m)的直线l,满足条件,则l的斜率必存在,进而可设直线方程与椭圆联立方程消去y,设A(x1,y1),B(x2,y2)根据判别式大于0求得m的范围,根据韦达定理可表示出x1+x2和x1x2,进而表示出
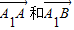 根据
根据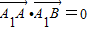 求得m的值,最后进行检验看m是否符合.
求得m的值,最后进行检验看m是否符合.解答:解:(1)依题意得:
 ,∴
,∴ ,∴b2=a2-c2=3
,∴b2=a2-c2=3∴所求的椭圆方程为:
 .
.(2)由(1)知,F1(0,1)则抛物线的方程为x2=4y
即

设
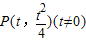 则该点处的切线的斜率
则该点处的切线的斜率
∴切线方程为
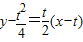
令
 令
令
∴
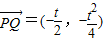

∴
 即
即 .
.(3)假设存在过点(0,m)的直线l,满足条件,则l的斜率必存在,
∴可设l方程为y=kx+m联立
 消去y得(4+3k2)x2+6mkx+3(m2-4)=0,
消去y得(4+3k2)x2+6mkx+3(m2-4)=0,设A(x1,y1),B(x2,y2)
则
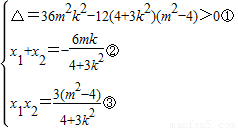
由①得4+3k2-m2>0
由②③及直线l的方程得y1y2=(kx1+m)(kx2+m)=k2x1x2+mk(x1+x2)+m2
=
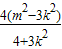 y1+y2=(kx1+m)+(kx2+m)=k(x1+x2)+2m
y1+y2=(kx1+m)+(kx2+m)=k(x1+x2)+2m=

∵椭圆的上顶点为A1(0,2),

∴x1x2+(y1-2)(y2-2)=0即x1x2+y1y2-2(y1+y2)+4=0
∴

整理得7m2-16m+4=0解得

当m=2时,直线l的方程为y=kx+2过椭圆的上顶点A1(0,2)与已知矛盾
当
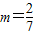 时,直线l的方程为
时,直线l的方程为 符合题意
符合题意∴存在过点(0,m)的直线l,使得l与椭圆相交于A、B两点,且满足
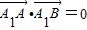 ,实数m的值为
,实数m的值为
点评:本题主要考查了椭圆的标准方程和直线与椭圆的关系.考查了学生对圆锥曲线知识的综合掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、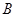 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.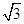
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线