题目内容
设复数z1,z2在复平面上(O为原点)对应的点分别为Z1(sinθ,1),Z2(1,cosθ),其中-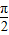 <θ<
<θ< ,
,(1)若
 ⊥
⊥ ,求θ;
,求θ;(2)若
 =
=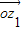 +
+ ,求点Z的轨迹的普通方程;并作出轨迹示意图.
,求点Z的轨迹的普通方程;并作出轨迹示意图.(3)求|OZ1+OZ2|的最大值.
【答案】分析:(1)根据两个向量之间的垂直关系,得到对应的向量的数量积等于0,得到关于三角函数的等式,求出正切值,根据角的范围得到角的大小.
(2)根据复数相等的充要条件,写出复数的实部和虚部分别相等,得到关于三角函数的等式,去掉字母参数,得到圆的方程,根据三角函数做出x,y的范围,画出图形.
(3)要求模长的最值.需要根据所给的复数的表示形式,求出复数的模长的表示式,根据三角函数的最值的求法,得到复数的模长的最值.
解答:2解(1)∵由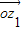 ⊥
⊥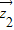 ,知
,知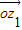 •
•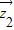 =0
=0
∴sinθ+cosθ=0
∴tanθ=-1
∵-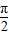 <θ<
<θ<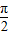
∴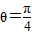
(2)设Z(x,y)
则有(x,y)=(sinθ,1)+(1,cosθ)
=(1+sinθ,1+cosθ)
∴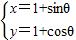 ,中-
,中-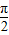 <θ<
<θ<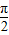
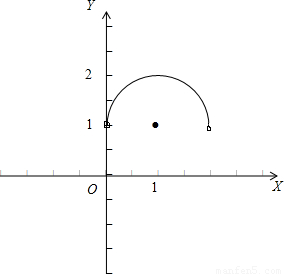
消去θ得:(x-1)2+(y-1)2=1(1<y≤2)
(3)|OZ1+OZ2|=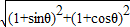
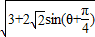
∵-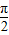 <θ<
<θ<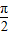
∴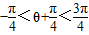
∴-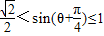
可求得|OZ1+OZ2|的最大值为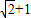
点评:本题考查复数与向量的综合题目,考查复数的几何意义,考查三角函数的最值和恒等变形,本题解题的关键是题目的每一个环节都不是难题,但是容易在这种小的细节处出错,本题是一个易错题.
(2)根据复数相等的充要条件,写出复数的实部和虚部分别相等,得到关于三角函数的等式,去掉字母参数,得到圆的方程,根据三角函数做出x,y的范围,画出图形.
(3)要求模长的最值.需要根据所给的复数的表示形式,求出复数的模长的表示式,根据三角函数的最值的求法,得到复数的模长的最值.
解答:2解(1)∵由
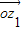 ⊥
⊥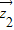 ,知
,知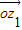 •
•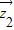 =0
=0∴sinθ+cosθ=0
∴tanθ=-1
∵-
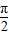 <θ<
<θ<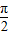
∴
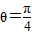
(2)设Z(x,y)
则有(x,y)=(sinθ,1)+(1,cosθ)
=(1+sinθ,1+cosθ)
∴
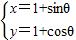 ,中-
,中-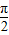 <θ<
<θ<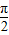

消去θ得:(x-1)2+(y-1)2=1(1<y≤2)
(3)|OZ1+OZ2|=
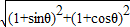
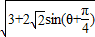
∵-
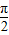 <θ<
<θ<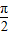
∴
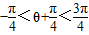
∴-
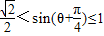
可求得|OZ1+OZ2|的最大值为
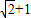
点评:本题考查复数与向量的综合题目,考查复数的几何意义,考查三角函数的最值和恒等变形,本题解题的关键是题目的每一个环节都不是难题,但是容易在这种小的细节处出错,本题是一个易错题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目