题目内容
某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试.在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为 ;
;(1)求该小组中女生的人数;
(2)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
 ,每个男生通过的概率均为
,每个男生通过的概率均为 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量ξ,求ξ的分布列和数学期望.
【答案】分析:(1)设出该小组中有n个女生,根据古典概型的概率公式得到比值,等于恰为一男一女的概率,解出关于n的方程.
(2)由题意知ξ的取值为0,1,2,3,集合变量对应的事件,和独立重复试验的概率公式,得到变量对应的概率,写出分布列,求出期望值.
解答:解:(1)设该小组中有n个女生,根据题意,得
解得n=6,n=4(舍去),
∴该小组中有6个女生;
(2)由题意,ξ的取值为0,1,2,3;
P(ξ=0)=
P(ξ=1)=
P(ξ=3)=
P(ξ=2)=1-
∴ξ的分布列为:
∴Eξ=1×
点评:本题考查离散型随机变量的分布列和期望,考查古典概型的概率公式,考查独立重复试验的概率公式,考查利用概率与统计的知识解决实际问题.
(2)由题意知ξ的取值为0,1,2,3,集合变量对应的事件,和独立重复试验的概率公式,得到变量对应的概率,写出分布列,求出期望值.
解答:解:(1)设该小组中有n个女生,根据题意,得

解得n=6,n=4(舍去),
∴该小组中有6个女生;
(2)由题意,ξ的取值为0,1,2,3;
P(ξ=0)=

P(ξ=1)=

P(ξ=3)=

P(ξ=2)=1-

∴ξ的分布列为:
| ξ | 1 | 2 | 3 | |
| P |  |  |  |  |

点评:本题考查离散型随机变量的分布列和期望,考查古典概型的概率公式,考查独立重复试验的概率公式,考查利用概率与统计的知识解决实际问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为 ,每个男生通过的概率均为
,每个男生通过的概率均为 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量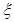 ,求
,求