题目内容
方程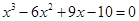 的实根个数是( )
的实根个数是( )
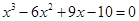 的实根个数是( )
的实根个数是( )| A.3 | B.2 | C.1 | D.0 |
C
试题分析:令f(x)=x3-6x2+9x-10,则f′(x)=3x2-12x+9=3(x-1)(x-3).
由f′(x)>0得x>3或x<1,
由f′(x)<0得1<x<3.
∴f(x)的单调增区间为(3,+∞),(-∞,1),单调减区间为(1,3),
∴f(x)在x=1处取极大值,在x=3处取极小值,
又∵f(1)=-6<0,f(3)=-10<0,
∴函数f(x)的图象与x轴有一个交点,
即方程x3-6x2+9x-10=0有一个实根.
故选C.
点评:中档题,利用转化思想,将方程根的个数的讨论,转化成函数零点个数的讨论,通过研究函数的单调区间及极值情况,确定函数图象与x轴的交点个数。

练习册系列答案
相关题目
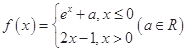 ,若函数
,若函数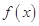 在
在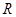 上有两个零点,则
上有两个零点,则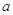 的取值范围是
的取值范围是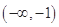
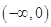
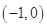
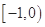
 :
:
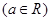 .若存在实数
.若存在实数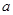 使得一条曲线与直线
使得一条曲线与直线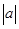 ,则称此曲线为直线
,则称此曲线为直线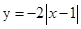 ;②
;②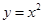 ;③
;③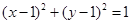 ;④
;④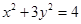 ;则其中直线
;则其中直线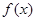 的定义域为
的定义域为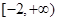 ,部分对应值如下表,函数
,部分对应值如下表,函数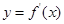 的大致图像如下图所示,则函数
的大致图像如下图所示,则函数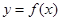 在区间
在区间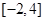 上的零点个数为( )
上的零点个数为( )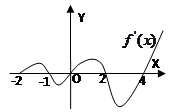
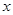
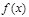
 的零点依次为a,b,c,则( )
的零点依次为a,b,c,则( )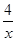 的零点是( )
的零点是( )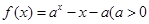 且
且 有两个零点,则实数
有两个零点,则实数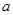 的取值范围是 .
的取值范围是 . 的零点所在区间是( )
的零点所在区间是( ) 



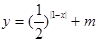 存在零点,则m的取值范围是__________.
存在零点,则m的取值范围是__________.