题目内容
用0到9这十个数字,可组成多少个没有重复数字的四位偶数?
2 296(个).
这一问题的限制条件是①没有重复数字;②数字“0”不能排在千位上;③个位数字只能是0、2、4、6、8.从限制条件入手,可划分如下:
如果从个位数入手,四位偶数可分为个位数是“0”的四位偶数;个位数是2、4、6、8的四位偶数.这是因为零不能放在千位数上,由此得解法一和解法二.
如果从千位数入手,四位偶数可分为千位数是1、3、5、7、9和千位数是2、4、6、8两类,由此得解法三.
如果四位数划分为四位奇数和四位偶数两类,先求出四位奇数的个数,用排除法,得解法四.
解法一:当个位上排“0”时,千位、百位、十位上可以从余下的九个数字中任选三个来排列,故有 个;
个;
当个位上在“2、4、6、8”中任选一个来排、则千位上从余下的八个非零数字中任意选一个、百位、十位上再从余下的八个数字中任选两个来排、按分步计数原理有 个.
个.
没有重复数字的四位偶数有 ="504+1" 792="22" 96(个).
="504+1" 792="22" 96(个).
解法二:当个位数字排0时,同解法一有 个;当个位数字是2、4、6、8之一时,千位、百位、十位上可从余下的九个数字中任选三个的排列中减去千位数是“0”的排列数、得
个;当个位数字是2、4、6、8之一时,千位、百位、十位上可从余下的九个数字中任选三个的排列中减去千位数是“0”的排列数、得 个.
个.
没有重复数字的四位偶数有 ="504+1" 792="2" 296(个).
="504+1" 792="2" 296(个).
解法三:千位上从1、3、5、7、9中任选一个,个位上从0、2、4、6、8中任选一个,百位、十位上从余下的八个数字中任选两个作排列,有 个;
个;
千位上从2、4、6、8中任选一个,个位上从余下的四个偶数中任选一个(包括0在内),百位、十位上从余下的八个数字中任意选两个作排列,有 个.
个.
没有重复数字的四位偶数有 ="2" 296(个).
="2" 296(个).
解法四:将没有重复数字的四位数划分为两类:四位奇数和四位偶数.没有重复数字的四位数有 个.
个.
其中四位奇数有 个,没有重复数字的四位偶数有
个,没有重复数字的四位偶数有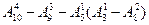 ="2" 296(个).
="2" 296(个).
如果从个位数入手,四位偶数可分为个位数是“0”的四位偶数;个位数是2、4、6、8的四位偶数.这是因为零不能放在千位数上,由此得解法一和解法二.
如果从千位数入手,四位偶数可分为千位数是1、3、5、7、9和千位数是2、4、6、8两类,由此得解法三.
如果四位数划分为四位奇数和四位偶数两类,先求出四位奇数的个数,用排除法,得解法四.
解法一:当个位上排“0”时,千位、百位、十位上可以从余下的九个数字中任选三个来排列,故有
 个;
个;当个位上在“2、4、6、8”中任选一个来排、则千位上从余下的八个非零数字中任意选一个、百位、十位上再从余下的八个数字中任选两个来排、按分步计数原理有
 个.
个.没有重复数字的四位偶数有
 ="504+1" 792="22" 96(个).
="504+1" 792="22" 96(个).解法二:当个位数字排0时,同解法一有
 个;当个位数字是2、4、6、8之一时,千位、百位、十位上可从余下的九个数字中任选三个的排列中减去千位数是“0”的排列数、得
个;当个位数字是2、4、6、8之一时,千位、百位、十位上可从余下的九个数字中任选三个的排列中减去千位数是“0”的排列数、得 个.
个.没有重复数字的四位偶数有
 ="504+1" 792="2" 296(个).
="504+1" 792="2" 296(个).解法三:千位上从1、3、5、7、9中任选一个,个位上从0、2、4、6、8中任选一个,百位、十位上从余下的八个数字中任选两个作排列,有
 个;
个;千位上从2、4、6、8中任选一个,个位上从余下的四个偶数中任选一个(包括0在内),百位、十位上从余下的八个数字中任意选两个作排列,有
 个.
个.没有重复数字的四位偶数有
 ="2" 296(个).
="2" 296(个).解法四:将没有重复数字的四位数划分为两类:四位奇数和四位偶数.没有重复数字的四位数有
 个.
个.其中四位奇数有
 个,没有重复数字的四位偶数有
个,没有重复数字的四位偶数有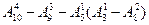 ="2" 296(个).
="2" 296(个).
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目



 种
种 种
种


 ?
?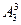
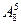 种
种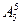
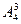 种
种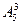 种
种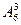 种
种