题目内容
已知:矩形AEFD的两条对角线相交于点M(2,0),AE边所在直线的方程为:x﹣3y﹣6=0,点T(﹣1,1)在AD边所在直线上.
(1)求矩形AEFD外接圆P的方程.
(2)△ABC是⊙P的内接三角形,其重心G的坐标是(1,1),求直线BC的方程.
(1)求矩形AEFD外接圆P的方程.
(2)△ABC是⊙P的内接三角形,其重心G的坐标是(1,1),求直线BC的方程.
解:(1)设A点坐标为(x,y)
∵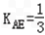 且 AE⊥AD,
且 AE⊥AD,
∴KAD=﹣3又T(﹣1,1)在AD上,
∴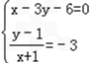 ,
,
∴ 即A点的坐标为(0,﹣2)
即A点的坐标为(0,﹣2)
又∵M点是矩形AEFD两条对角线的交点,
∴M点(2,0)即为矩形AEFD外接圆的圆心,其半径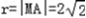
∴⊙P的方程为(x﹣2)2+y2=8
(2)连AG延长交BC于点N(x0,y0),则N点是BC中点,连MN
∵G是△ABC的重心,
∴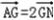 ,
,
∴(1,3)=2(x0﹣1,y0﹣1),
∴
∵M是圆心,N是BC中点,
∴MN⊥BC,且 KMN=﹣5,
∴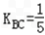 ,
,
∴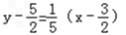 即直线BC的方程为x﹣5y+11=0
即直线BC的方程为x﹣5y+11=0
∵
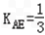 且 AE⊥AD,
且 AE⊥AD,∴KAD=﹣3又T(﹣1,1)在AD上,
∴
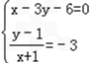 ,
,∴
 即A点的坐标为(0,﹣2)
即A点的坐标为(0,﹣2)又∵M点是矩形AEFD两条对角线的交点,
∴M点(2,0)即为矩形AEFD外接圆的圆心,其半径
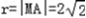
∴⊙P的方程为(x﹣2)2+y2=8
(2)连AG延长交BC于点N(x0,y0),则N点是BC中点,连MN
∵G是△ABC的重心,
∴
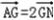 ,
,∴(1,3)=2(x0﹣1,y0﹣1),
∴

∵M是圆心,N是BC中点,
∴MN⊥BC,且 KMN=﹣5,
∴
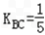 ,
,∴
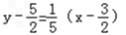 即直线BC的方程为x﹣5y+11=0
即直线BC的方程为x﹣5y+11=0
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目