题目内容
双曲线的左焦点为F1，顶点为A1、A2，P是双曲线上任意一点，则分别以线段PF1、A1A2为直径的两圆的位置关系为（ ）
分析：画出图象，考查两圆的位置关系，就是看圆心距与半径和或与半径差的关系，分情况P在左支、右支，推导结论．
解答：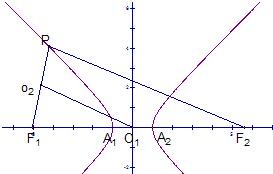
解：设以线段PF1、A1A2为直径的两圆的半径
分别为r1、r2，
若P在双曲线坐支，如图所示，
则|O1O2|=
|PF2|=
（|PF1|+2a）
=
|PF1|+a=r1+r2，
即圆心距为半径之和，两圆外切．
若P在双曲线右支，同理求得|O1O2|=r1-r2，
故此时，两圆相内切．
综上，两圆相切，
故选B．
解：设以线段PF1、A1A2为直径的两圆的半径分别为r1、r2，
若P在双曲线坐支，如图所示，
则|O1O2|=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
即圆心距为半径之和，两圆外切．
若P在双曲线右支，同理求得|O1O2|=r1-r2，
故此时，两圆相内切．
综上，两圆相切，
故选B．
点评：本题考查圆与圆的位置关系及其判定，双曲线的定义和简单性质的应用，考查数形结合思想方法，是中档题．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
已知双曲线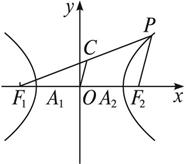
的左焦点为F1,左、右顶点为A1、A2,P为双曲线上任意一点,则分别以线段PF1、A1A2为直径的两个圆的位置关系为( )
的左焦点为F1,与x轴的交点为A1、A2,P是双曲线上任意一点,则分别以线段PF1、A1A2为直径的两圆的位置关系为( )
的左焦点为F1，左、右顶点分别为A1、A2，P为双曲线上任意一点，则分别以线段PF1，A1A2为直径的两个圆的位置关系为（ ）